Алгебра, вопрос задал garov1lya , 6 лет назад

Помогите плиз. Неравенства с степенями 3 выражения. помогите прошу !!

Приложения:

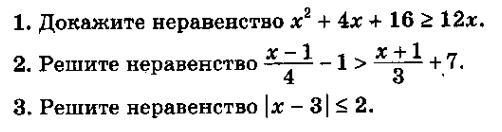
Ответы на вопрос

Ответил Applegate

Ответ:

$1)$ неравенство доказано (см.объяснение);

$2)x\in(-\infty;-103)$

$3) x\in[1;5]$

Объяснение:

$\boxed{1.}$ выделим полный квадрат согласно ФСУ $(a\pm b)^2=a^2\pm2ab+b^2:$

$x^2+4x+16\geq 12x;\\x^2+4x+16-12x\geq 0;\\x^2-8x+16\geq 0;\\(x-4)^2\geq 0$

число в четной степени всегда либо положительно,либо равно нулю.неравенство доказано.

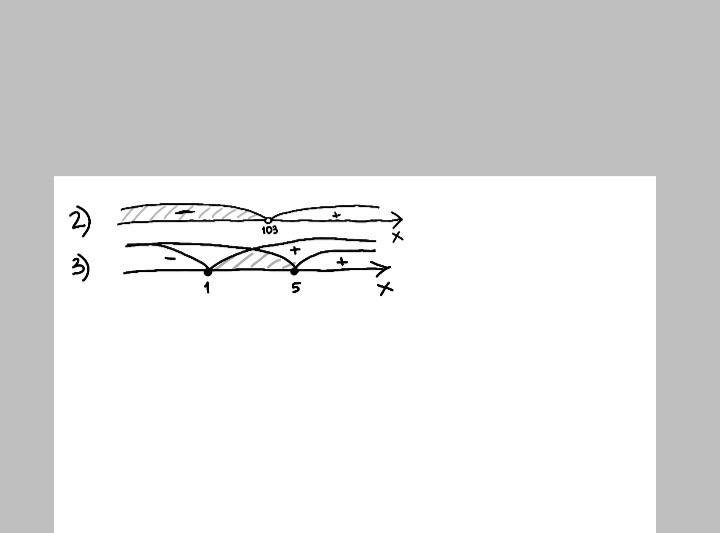
$\boxed{2.} ~~~\displaystyle \frac{x-1^{(3}}{4} -1^{(12} > \frac{x+1^{(4}}{3} +7^{(12};\\~~3x-3-12 > 4x+4+84;\\-15 > 4x-3x+88;\\-15-88 > x;\\x < -103;\\x\in(-\infty;-103)$

чертеж на изображении.

$\boxed{3.}~~~|x-3|\leq 2$ раскроем модуль. имеем два случая:

$1)~~\displaystyle x-3\leq 2;\\x\leq 2+3;\\\ x\leq 5;\\\ x\in(-\infty;5]\\\\2) x-3\geq -2;\\ x\geq -2+3;\\\ x \geq 1;\\\ x\in[1;+\infty)$

чертеж на изображении.

находим объединение промежутков решений обоих случаев,это и будет ответом: $1\leq x\leq 5$ или $x\in[1;5]$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Подyмайте и запишите продолжения следующих предложений. Мне трудно ... Я радyюсь ... Пpи общении я стараюcь ... Я огорчаюсь ... Для меня очень важно...

Русский язык, 1 год назад

помогите пожалуйста даю 40 баллов с каждым сочетаниям:согласна кодексу,исключая двоих,на хорошей работе.Придумайте 3-4 предложения...

География, 6 лет назад

срочно аааааааааааааааааа...

Українська література, 6 лет назад

Кр, помогите пожалуйса ...

Биология, 8 лет назад

Охарактеризуйте представителей класса Ракообразные.

История, 8 лет назад

Какие обвинения выдвинул московский князь Юрий Данилович против своего политического соперника Михаила Тверского?