ПОМОГИТЕ ПЛИИЗ СРОЧНО ДАМ 20 БАЛЛОВ!!!
С ДАНО И ДОКАЗАТЕЛЬСТВО!!
​

Здравствуй kokobobo!

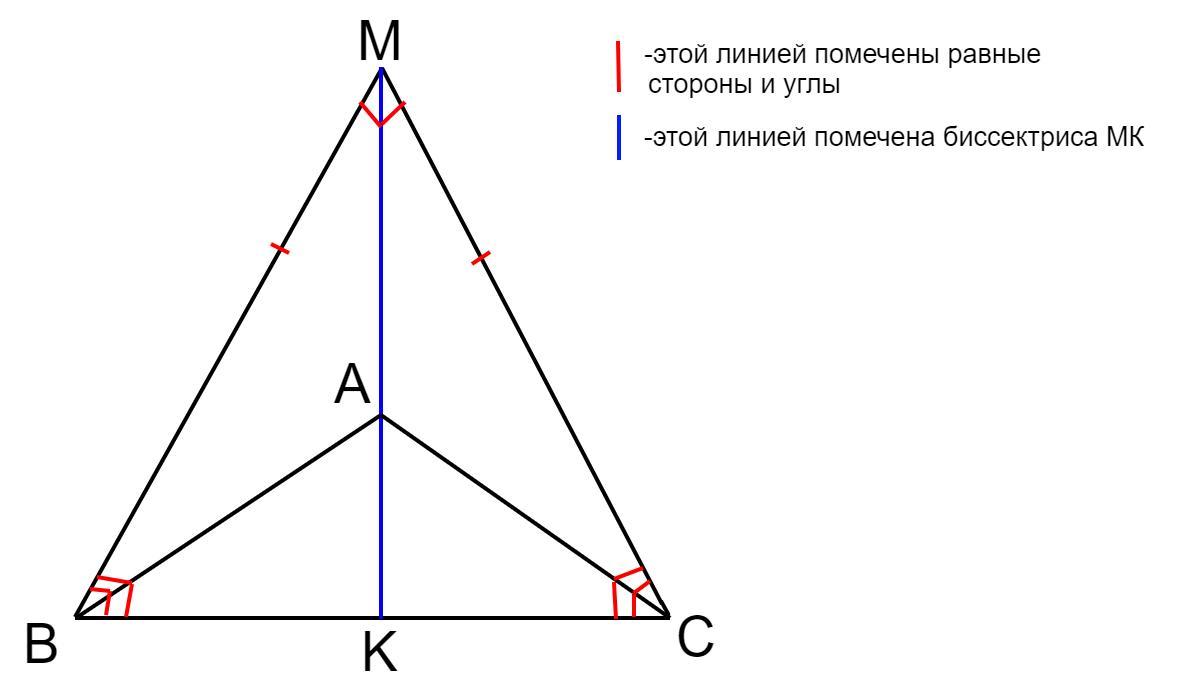
В треугольнике ВМС стороны ВМ и МС равны, точка А лежит на биссектрисе МК, Докажите, что АВ=АС

Для начала запишем известные нам условия

Дано:

ΔBMC

BM=MC

∠BMK=∠CMK

MK-биссектриса

A∈MK  

Доказать

АВ=АС

Доказательство:

Так как BM=MC, то из этого следует что, ΔBMC-равнобедренный.

Так как этот треугольник равнобедренный, то вспомним свойство равнобедренных треугольников: "В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой."

Тогда:

1) Биссектриса MK является медианой, откуда следует BK=KC

2) Биссектриса MK является высотой, откуда следует, что треугольники AKB и AKC прямоугольные.

В прямоугольных треугольниках AKB и AKC катет AK общий, а катеты BK и KC равны. Тогда, по признаку равенства прямоугольных треугольников по двум катетам треугольники AKB и AKC равны, отсюда АВ = АС. Ч.т.д.

Другой вид доказательства данной задачи

Дано:

ΔBMC

BM=MC

∠BMK=∠CMK

MK-биссектриса

A∈MK  

Доказать

АВ=АС

Доказательство:

1) ΔBMC- равнобедренный, так как BM=MC (по условию)

2) MK - медиана (по свойствам равнобедренного треугольника, *которая звучит так: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой*)

3) BK=KC, так как MK медиана

4) ΔAKB и AKC - прямоугольные, так как МК высота (по свойству равнобедренного треугольника)

5) Рассмотрим треугольники AKB и AKC

AK общий (по условию)

BK=KC (по условию можно написать)

Значит, ΔAKB = ΔAKC (по I признаку равенства прямоугольного треугольника, *который звучит так: Если катеты одного треугольника соответственно равны катетам другого треугольника, то такие прямоугольные треугольники равны*) Отсюда следует, что АВ = АС.

Что и требовалось доказать.

То что написано внутри звездочек (**) писать не обязательно, этим я показал как звучат те или иные формулы и теоремы.

Удачи в последующих задачах!