помогите, не могу решить​

Ответ

DF = см

Объяснение:

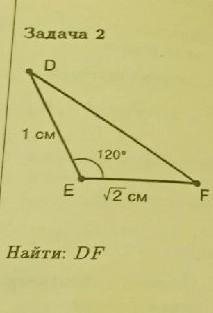
Дано: ∆EFD , ED = 1см , EF = √2см , ∠F = 120°

Найти: DF

          Решение:

Если известный угол находится между известными сторонами , то противолежащую сторону к этому углу можно найти с помощью теоремы косинусов.

DF² = ED² + EF² - 2 · ED · EF · cosα

α - градусная мера угла , лежащей ,  между двумя , известными , сторонами .

P.S : cos120° = - 1/2(по таблице тригонометрических функций)