Алгебра, вопрос задал Ruuі , 1 год назад

Помогите найти производную.
От меня лайк и подписка. ​

Приложения:

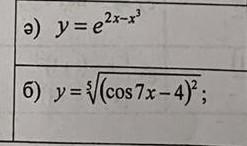
Ответы на вопрос

Ответил QDominus
1

1) Дана функция

y = {e}^{2x - {x}^{3} }

Эта функция является сложной, поэтому и дифференцировать её мы будем как сложную функцию:

\frac{d}{dx} ( {e}^{2x - {x}^{3} } ) = \frac{d}{dx} ( {e}^{2x - {x}^{3} } ) \times \frac{d}{dx} (2x - {x}^{3} ) = \\ = e^{2x - {x}^{3} } (2 - 3 {x}^{2} ) = 2 {e}^{2x - {x}^{3} } - 3 {x}^{2} e^{2x - {x}^{3} }

2) Дана функция

y = \sqrt[5]{ {( \cos(7x) - 4) }^{2} }

Эта функция является тоже сложной, поэтому и её мы будем дифференцировать аналогично, но сперва запишем радикал в виде степени:

\frac{d}{dx}( ( \cos(7x) - 4)^{ \frac{2}{5} } ) = \frac{d}{dx} (g(x) ^{ \frac{2}{5} } ) \times \frac{d}{dx} ( \cos(7x) - 4) = \\ = \frac{2}{5} g(x)^{ - \frac{3}{5} } \times( - \sin(7x) \times 7) = - \frac{2 \times 7}{5} ( \cos(7x) - 4)^{ - \frac{3}{5} } \sin(7x) = \\ = - \frac{14 \sin(7x) }{ 5\sqrt[5]{ {( \cos(7x - 4) )}^{3} } }

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Алгебра, 1 год назад
преобразуйте в многочлен (3-а)^2...
История, 1 год назад
воєні вміння татар та турків 16 ст...
Математика, 1 год назад
Прямолинейное движение материальной точки задано уравнением S(t)=8+2t-24t^2-0.3t^5 , (м). В какой момент времени скорость точки будет равна 2 м/с? Помогите с решением пожалуйста.
Физика, 1 год назад
Поезд через 10 с после начала движется приобритая скорость скорость 0.6м/с. Чему равна ускорение поезда?
Русский язык, 6 лет назад
Выпиши сложные слова и разбери их по составу...
География, 6 лет назад
Где наибольшая концентрация населения?