Помогите найти предел, пожалуйста срочно!!!!
Приложения:
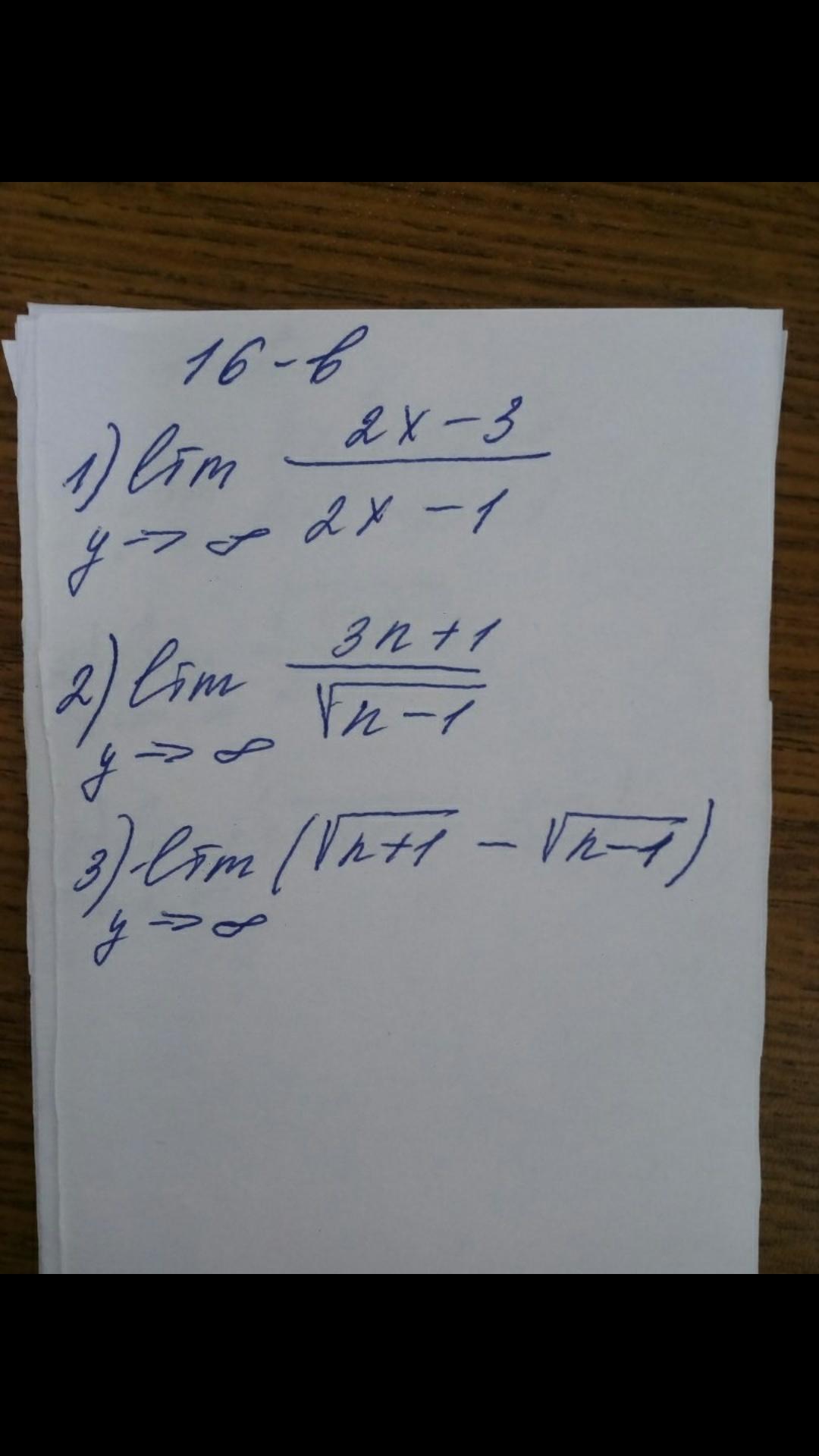
sergeybasso:
под знаком предела написан y, а выражения для x и n - формально тут считать нечего, выражение останется константой. Вероятно, аргумент стоило подписать другой ;)
Скорее всего ошибка учителя, но если не учитывать у? Как решать
Ответы на вопрос
Ответил sergeybasso
1
Ответ:
1) 1
2) +∞
3) 0
Объяснение:
1)
2)
В числителе бесконечно большая последовательность - ее предел = бесконечности, в знаменетале последовательность в пределе имеет 1 (сумма 1 и бесконечно малой) - значит итогом будет бесконечность.
3)
В знаменателе босконечно большая последовательность, как сумма бесконечно больших (оба корня стремятся к +∞) - значит 2 разделить на бесконечно большую будет бесконечно малая.
Спасибо большое!
Новые вопросы