Математика, вопрос задал 1234432200341 , 6 лет назад

Помогите найти предел пожалуйста не по правилу Лапиталя только.

Приложения:

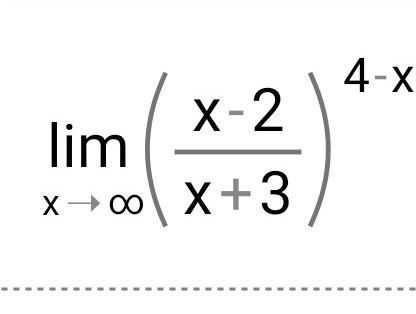
Ответы на вопрос

Ответил xERISx

Решение сводится к нахождению второго замечательного предела.

$\lim_{x \to \infty} \left(1+\dfrac 1x\right)^x=e$

=============================

Имеем неопределенность вида:

$\lim_{x \to \infty} \left(\dfrac {x-2}{x+3}\right)^{4-x}=\dfrac{\infty}{\infty}$

$\lim_{x \to \infty} \left(\dfrac {x-2}{x+3}\right)^{4-x}=\lim_{x \to \infty} \left(1+\dfrac {-5}{x+3}\right)^{4-x}=\\\\\\=\lim_{x \to \infty} \left(1+\dfrac1{\left(\dfrac{x+3}{-5}\right)}\right)^{4-x}=\\\\\\=\lim_{x \to \infty} \left(\left(1+\dfrac1{\left(\dfrac{x+3}{-5}\right)}\right)^{\left(\dfrac{x+3}{-5}\right)}\right)^{\left(\dfrac{-5}{x+3}\right)\cdot(4-x)}=(*)$

.............................................................................

Выражение в крупных скобках есть второй замечательный предел:

$x\rightarrow\infty\ \ \ \Rightarrow\ \ \ \left(\dfrac{x+3}{-5}\right)\rightarrow\infty\\\\\\\lim_{x \to \infty} \left(\left(1+\dfrac1{\left(\dfrac{x+3}{-5}\right)}\right)^{\left(\dfrac{x+3}{-5}\right)}\right)=e$

............................................................................

Тогда предел принимает вид:

$\displaystyle(*)=e^{\lim_{x \to \infty}\left(\frac{-5}{x+3}\right)\cdot(4-x)}=e^{\lim_{x \to \infty}\left(\frac{5x-20}{x+3}\right)}=\\\\=e^{\lim_{x \to \infty}\left(5-\frac{35}{x+3}\right)}=e^{5-0}=e^5\ \ \ \ \approx 148,4$