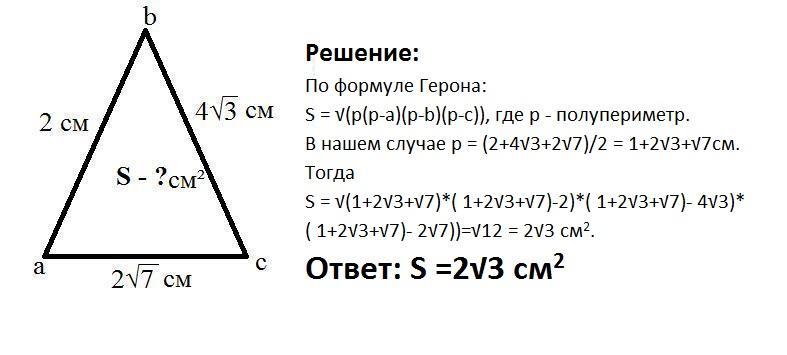
Помогите найти площу треугольника abc стороны ab=2 bc=4√3 ac=2√7
Ответы на вопрос
Если известны все три стороны треугольника ABC, то формула площади треугольника по трем сторонам: S=√p*(p-a)*(p-b)*(p-c)
где: p – полупериметр треугольника, a, b, c – длины сторон треугольника.
Периметр – это сумма длин всех сторон треугольника. Соответственно полупериметр – это сумма длин всех сторон разделенная на 2. Формула полупериметра: p=(a+b+c)/2.
Решение:
р = (2+4√3+2√7)/2 = 1+2√3+√7см.
Тогда
S = √(1+2√3+√7)*( 1+2√3+√7)-2)*( 1+2√3+√7)- 4√3)*( 1+2√3+√7)- 2√7))=√12 = 2√3 см2.
Ответ: S =2√3 см2
Рисунок в приложении...
Ответ:
Sabc = 2√3 ед²
Объяснение:
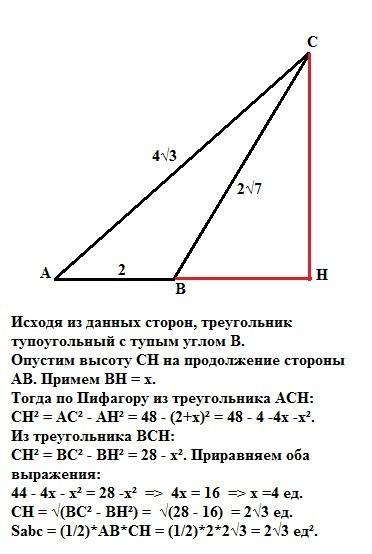
Исходя из теоремы Пифагора - если a² + b² < c² (где с - большая сторона), то треугольник тупоугольный, в нашем случае треугольник тупоугольный с тупым углом при вершине В.
Опустим высоту СН на продолжение стороны АВ.
Примем ВН = х.
Тогда по Пифагору из треугольника АСН:
СН² = АС² - (2+х)² = 48 - 4 -4х -х² = 44 - 4х -х².
Из треугольника ВСН по Пифагору:
СН² = ВС² - х² = 28 - х². Приравняем оба выражения:
44 - 4х -х² = 28 - х² => х = 4 ед. =>
СН = √(ВС² - х²) = √(28-16) = 2√3 ед.
Sabc = (1/2)*AB*CH = (1/2)*2*2√3 = 2√3 ед².