Математика, вопрос задал isherzodkon , 1 год назад

Помогите найти площадь с интегралом.

Приложения:

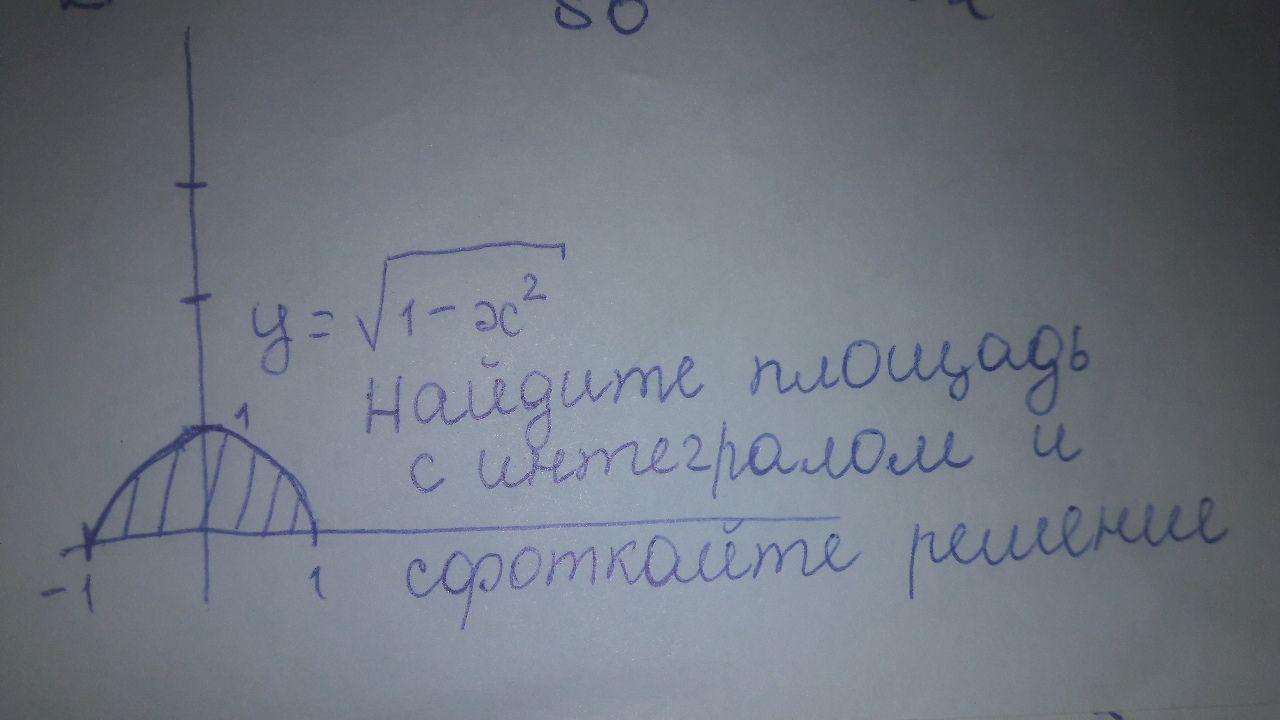
Ответы на вопрос

Ответил xxxeol

0

РЕШЕНИЕ
Пределы интегрирования: а = 1, b = -1
Вторая функция - y = 0
Находим интеграл РАЗНОСТИ функции
$S= \int\limits^1_b { \sqrt{1-x^2} } \, dx= \frac{arcsinX}{2}+ \frac{x \sqrt{1-x^2} }{2}= \frac{ \pi }{2}$
ОТВЕТ: Площадь π/2 ≈ 1,57
$S= \int\limits^a_b { \sqrt{1-x^2} } \, dx=- \frac{x}{ \sqrt{1-x^2} }$

Приложения:

isherzodkon: Как ты применил arcsin?

xxxeol: Добавил формулы - арксинус - от корня в знаменателе.

xxxeol: Это не сам Я рассчитывал.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 1 год назад

Вкажить коеффициент одночлена -2,7а2bd4 А) 2 Б) -2,7 В) 2,7 Г) 1...

Математика, 1 год назад

Автомобіль за перші 2 год проїхав 182 1/2км,а потім за 2 1/2 год проїхав 195 1/2 Знайди середню швидкість автомобіля на всьому шляху.

Математика, 1 год назад

В саду 48 яблони,груш в 3 раза меньше,чем яблонь,а слив на 16 больше,чем груш.Сколько всего фруктовых деревьев в этом саду Запиши решение задачи с кратким поеснением Очень нужно!!

Русский язык, 1 год назад

1. Загрязнение леса 2. Лесные пожары 3. Вырубка лесов 4. Загрязнение леса 5. Глобальное потепление 6. Мутации 7. Свалки мусора 8. Красная книга 9. Бездомные домашние животные 10. Выживание...

Обществознание, 6 лет назад

Как бы вы смогли рассказать 7 летнему ребенку о нарушении моральных и правовых норм? напишите какими словами бы вы смогли донести до него эту мысль.

Литература, 6 лет назад

на рисунке представляется экосистема а ) используя данную на рисунке экосистему выпишите не достоющие организмы в экологическую пирамиду б) объясните переход энергии и веществ в экологической...