помогите найти неравенство
Приложения:
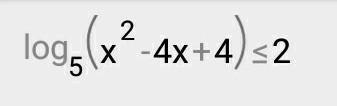
Ответы на вопрос
Ответил Trover
0
О.Д.З.:
Последнее условие выполняется при любых x.
Решение:
Ответил matilda17562
0
х отличен от двух.
Ответил matilda17562
0
Ответ неверный!
Ответил takushnir
0
ВОт.. где это неравенство найти?))))))))
㏒₅(х²-4х+4)≤2; х²-4х+4≥0(х-2)²≥0,
ОДЗ х≠2; т.к. основание 5 больше единицы, то х²-4х+4≤25⇒х²-4х-21≤0;
по теореме, обратной теореме Виета, корни левой части неравенства 7и -3, ______-3_______7______
+ - + Решение неравенства будет
[-3;7] с учетом ОДЗ решением исходного неравенста будет
[-3;2)∪(2;7]
Новые вопросы