Помогите мне пожалуйста с алгеброй, последняя надежда!!!
Приложения:
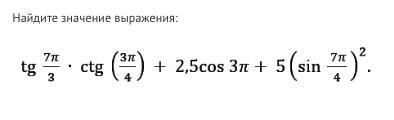
Ответы на вопрос
Ответил sofakrizanovskaa0
1
Ответ:
-√3
пожалуйста)))))))
Приложения:

romaprihodko2006:
Слушай, а ловко ты это придумала, я даже сначала не понял, молодец!
Ответил romaprihodko2006
1
Сначала просчитаем все функции по отдельности.
tg(7π/3)=tg(2π+π/3), т.к периодичность значений котангенса это π, то tg(2π+π/3)=tg(π/3), а это уже табличное значение. Это √3
ctg(3π/4). Периодичность котангенса также π, поэтому ctg(3π/4) это то же самое, что и ctg(7π/4). Угол 7π/4 равен -π/4. ctg(-π/4)=-ctg(π/4). Табличное значение. Это -1.
2.5cos(3π). Периодичность косинуса это 2π, поэтому 2.5cos(3π)=2.5cos(π).
Табличное значение. Это будет равно -2.5.
5(sin(7π/4)²). Угол 7π/4 равен углу -π/4. По свойству синуса (синус это непарная функция) sin(-π/4)=-sin(π/4). Табличное значение. Выходит 5sin²(7π/4)=5/2
Подставим значения.
√3 * (-1) + (-5/2) + 5/2
Выполнив арифметические действия выходит -√3
Ответ: -√3
tg(7π/3)=tg(2π+π/3), т.к периодичность значений котангенса это π, то tg(2π+π/3)=tg(π/3), а это уже табличное значение. Это √3
ctg(3π/4). Периодичность котангенса также π, поэтому ctg(3π/4) это то же самое, что и ctg(7π/4). Угол 7π/4 равен -π/4. ctg(-π/4)=-ctg(π/4). Табличное значение. Это -1.
2.5cos(3π). Периодичность косинуса это 2π, поэтому 2.5cos(3π)=2.5cos(π).
Табличное значение. Это будет равно -2.5.
5(sin(7π/4)²). Угол 7π/4 равен углу -π/4. По свойству синуса (синус это непарная функция) sin(-π/4)=-sin(π/4). Табличное значение. Выходит 5sin²(7π/4)=5/2
Подставим значения.
√3 * (-1) + (-5/2) + 5/2
Выполнив арифметические действия выходит -√3
Ответ: -√3
Новые вопросы
Українська мова,
1 год назад
Геометрия,
1 год назад
Українська мова,
1 год назад
Биология,
1 год назад
Математика,
6 лет назад