Помогите! Математика!
Приложения:
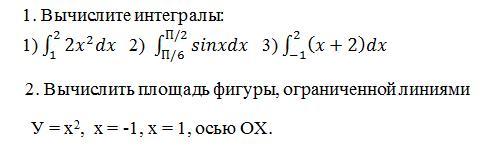
Ответы на вопрос
Ответил mionkaf1
1
Приложения:
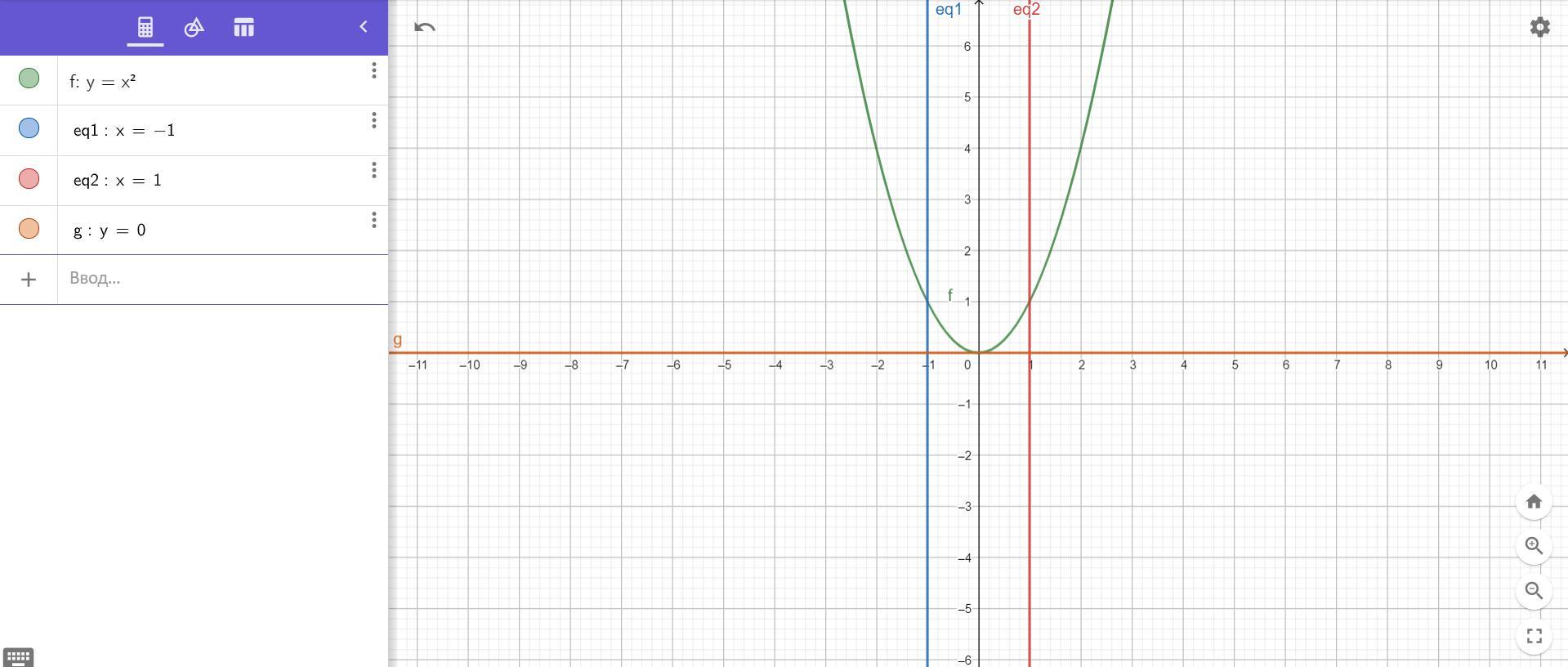
Новые вопросы
https://znanija.com/task/37723637?utm_source=android&utm_medium=share&utm_campaign=question