Помогите! Как решить неопределённый интеграл?
Приложения:
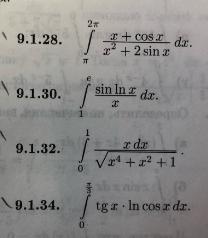
Ответы на вопрос
Ответил shavrinatv
0
Это определенный интеграл.
Решается заменами.
Приложения:


Ответил NNNLLL54
0
Приложения:


Ответил Аноним
0
привет
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Химия,
7 лет назад
Физика,
7 лет назад
Химия,
8 лет назад