Помогите!! Это очень срочно!!! Спасибо Вам заранее!

 

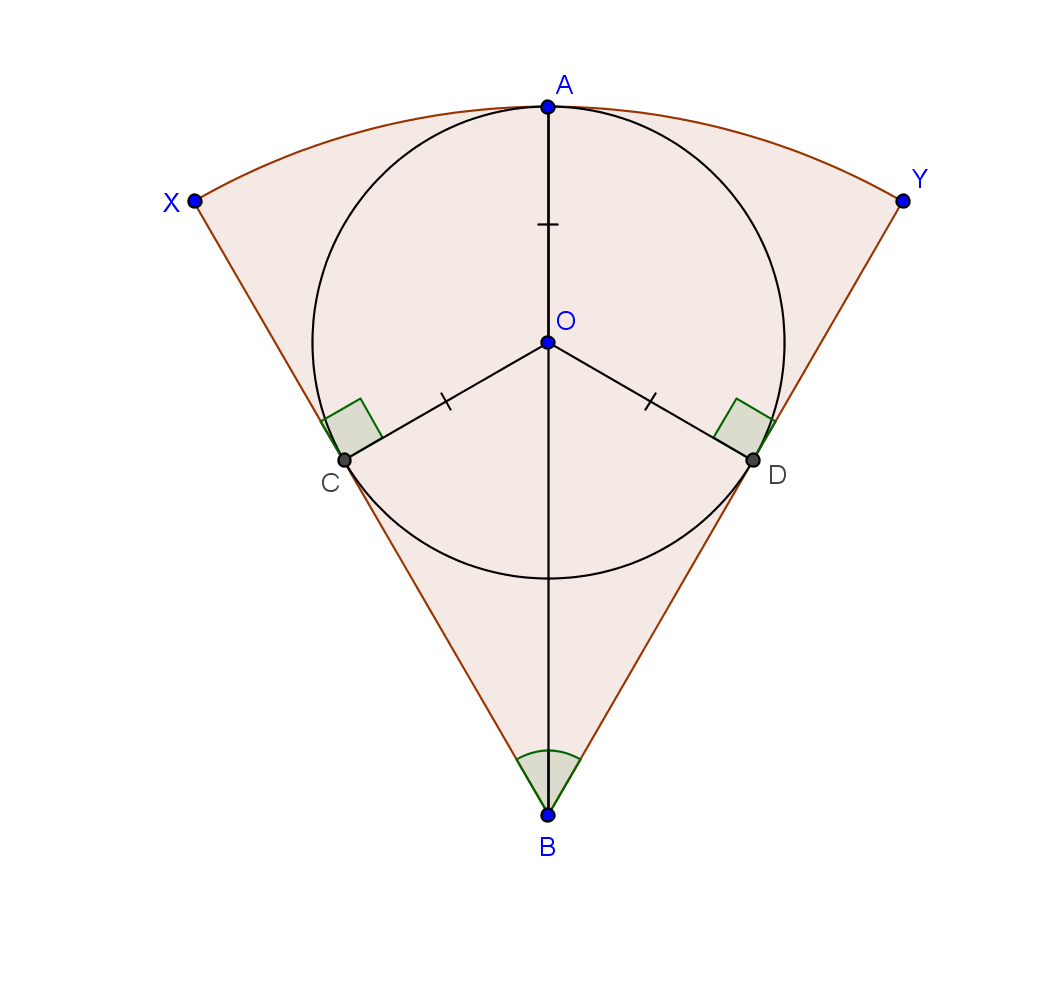
1)Найти площадь круга, вписанного в сектор, который ограничен радиусами по 4 см и дугой 60 гр.

 

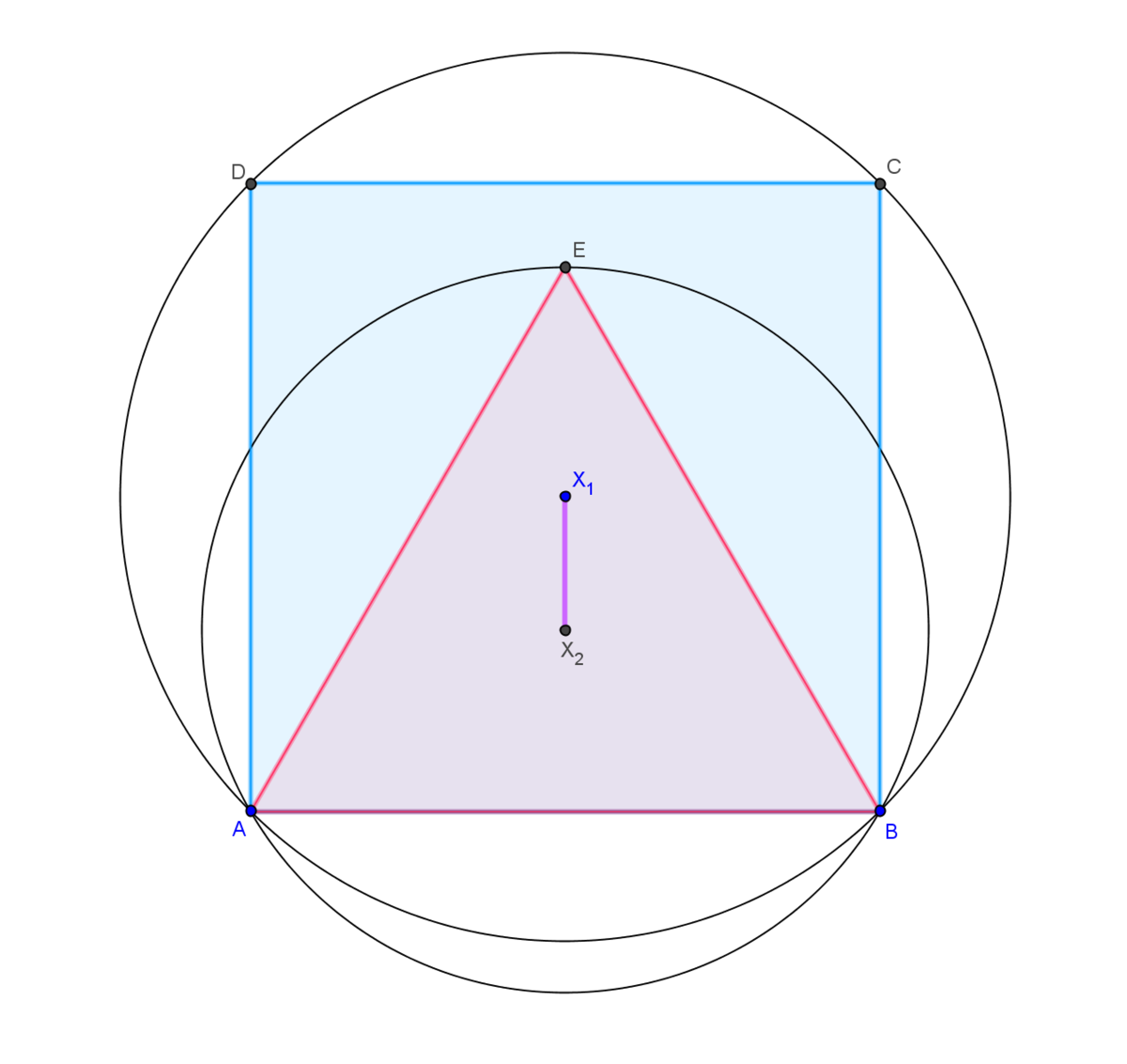
2)Центры двух перечекающихся окружностнй расположены по одну сторону от их общей хорды. Хорда=а и служит в одной окружности стороной правильного вписанного треугольника, а в другой-вписанного квадрата. Найдите расстояние между центрами этих окружностнй.

 

 

Помогитеее)

1) По симметрии: Центр лежит на отрезке АВ. Пусть центр в точке О. Тогда AO = OD = OC = r. Но OC лежит в треугольнике BOC против угла в 30 градусов, тогда OB = 2OC = 2r. 
AO + OB = r + 2r = 3r = R; r = R/3 = 4/3
S = pi*R^2 = 16pi/9
2) X1 с очевидностью отстоит от АВ на а/2.
Х2: расстояние равно разности между высотой треугольника h и радиусом описанной окружности R.
h = sqrt(3)/2 * a
R = a*sqrt(3)/3

Искомое расстояние a * (1/2 - sqrt(3)/2 + sqrt(3)/3) = a * (1/2 - sqrt(3)/6)

Спасибо!!!!!!