Помогите дорешать уравнение
Приложения:
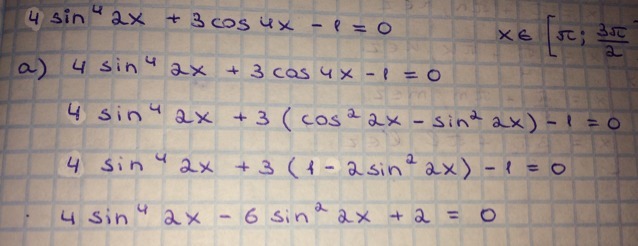
Ответы на вопрос
Ответил NNNLLL54
0
Новые вопросы
Другие предметы,
1 год назад
Физкультура и спорт,
1 год назад
Английский язык,
1 год назад
Алгебра,
1 год назад
Математика,
7 лет назад
Литература,
7 лет назад