Математика, вопрос задал miroslavxxx , 2 года назад

ПОМОГИТЕ Диференціальні рівняння. Помогите решить

Приложения:

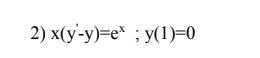
Ответы на вопрос

Ответил pushpull

Ответ:

y(x) = eˣ * ln(x)

Пошаговое объяснение:

Будем преобразовывать на ше уравнение.

Поделим обе части на хеˣ

$\displaystyle \large \boldsymbol { e^{-x}(y'-y)=\frac{1}{x} }\\\\\\\large \boldsymbol { e^{-x}y'-e^{-x}y=\frac{1}{x} }\\\\$

Представим - е⁻ˣ = (е⁻ˣ)'

$\displaystyle \ \large \boldsymbol { e^{-x}y'+(e^{-x})'y=\frac{1}{x} }\\\\$

Теперь к левой части применим формулу f'g + fg' = (fg)'

f = y; g= е⁻ˣ

$\displaystyle \ \large \boldsymbol { (y*e^{-x})'=\frac{1}{x} }\\\\$

Вот, собственно, и всё.

Проинтегрируем обе части уравнения

$\displaystyle \ \large \boldsymbol { \int {(y(x)*e^{-x})'} \, dx }=\int \frac{1}{x} \, dx \\\\$

$\displaystyle \large \boldsymbol { e^{-x} *y(x) = ln(x) +C}\\\\\\\large \boldsymbol {y(x) = e^x(ln(x)+C }$

Теперь используем начальное условие

y(1) = e¹(ln(1) +C) =0

e*C=0 ⇒ C = 0

Следовательно, наш ответ

y(x) = eˣ * ln(x)

#SPJ1

Новые вопросы

Другие предметы, 1 год назад

Қазақ тiлi, 1 год назад

Алгебра, 2 года назад

Физика, 2 года назад

Математика, 7 лет назад

Алгебра, 7 лет назад