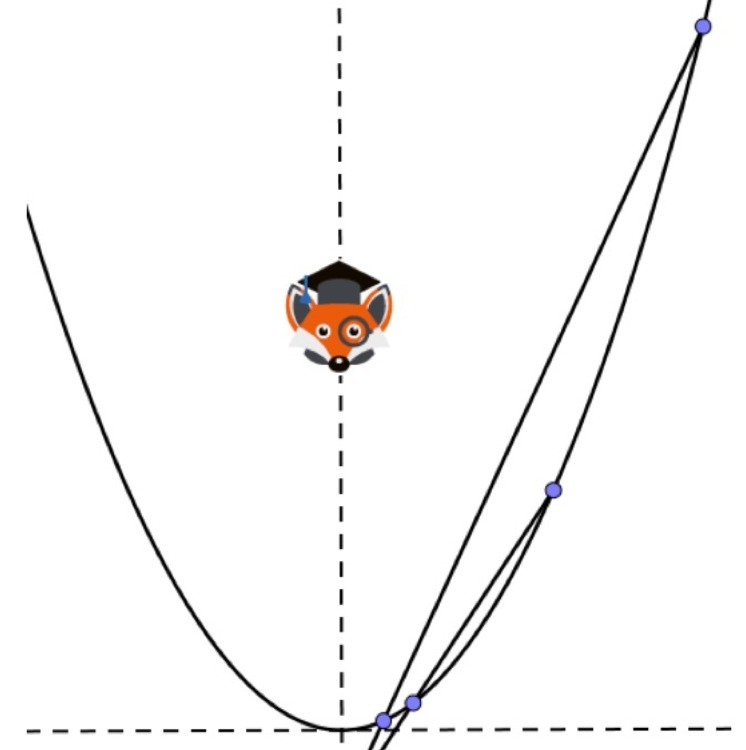
ПОМОГИТЕ ДАЮ МНОГО БАЛЛОВ!!! Мистер Фокс нарисовал параболу y=x^2 и отметил на ней четыре точки K , L , M и N . Оказалось, что точки выбраны им так, что прямые KL и M N пересеклись на оси ординат. Чему равна абсцисса точки N , если абсциссы точек K , L и M соответственно равны 5, 3 и 2?
Приложения:
Ответы на вопрос
Ответил oganesbagoyan
0
K(5; 25) , L(3;9) ,M(2;4) , N(t ; t²).
* * *K , L ,M и N ∈ графику функции y =x ² * * *
-----
t -?
Уравнение прямой проходящей через точки K(5; 25) и L(3;9) :
y =k*x +b ;
{ 25 =k*5+b ; 9 =k*3+b .⇔{ k =(25-9)/(5-3) ; b =25 - k*5 .⇔{ k =8 ; b= - 15.
y =8x - 15 . Точка C (0 ; -15) пересечение этой прямой с осью ординат.
Уравнение прямой проходящей через точки M(2; 4) и N(t ; t²) :
y =k₁*x+b₁ , где b₁ = b = - 15.
{ 4 =k*2- 15 ; t²=k*t-15 .⇔{ k =19/2 ; t²=(19/2)*t -15 .
---
t²=(19/2)*t -15 ⇔
2t²-19t +30 =0 ; D =19² -4*2*30 =361 -240 =121 =11²
t₁ = (19 -11)/2*2 = 2 ≡ x(M)
t₂ =(19+11)/4 =7,5.
ответ : 7,5. * * * N(7,5 ; 56,25) * * *
* * *K , L ,M и N ∈ графику функции y =x ² * * *
-----
t -?
Уравнение прямой проходящей через точки K(5; 25) и L(3;9) :
y =k*x +b ;
{ 25 =k*5+b ; 9 =k*3+b .⇔{ k =(25-9)/(5-3) ; b =25 - k*5 .⇔{ k =8 ; b= - 15.
y =8x - 15 . Точка C (0 ; -15) пересечение этой прямой с осью ординат.
Уравнение прямой проходящей через точки M(2; 4) и N(t ; t²) :
y =k₁*x+b₁ , где b₁ = b = - 15.
{ 4 =k*2- 15 ; t²=k*t-15 .⇔{ k =19/2 ; t²=(19/2)*t -15 .
---
t²=(19/2)*t -15 ⇔
2t²-19t +30 =0 ; D =19² -4*2*30 =361 -240 =121 =11²
t₁ = (19 -11)/2*2 = 2 ≡ x(M)
t₂ =(19+11)/4 =7,5.
ответ : 7,5. * * * N(7,5 ; 56,25) * * *
Новые вопросы
Английский язык,
2 года назад
Английский язык,
2 года назад
Математика,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад