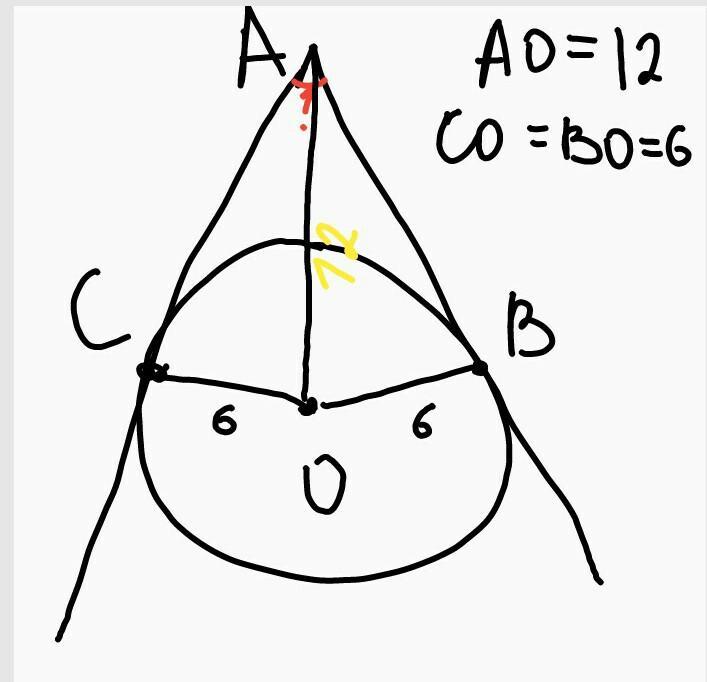
Помогите, даю 98 баллов! AC и AB - касательные, проведенные к окружности с центром в точке O и радиусом 6, C и B – точки касания. Найдите угол BAC, если AO=12. Пожалуйста, сделайте на листочке, достойно и качественно!
Ответы на вопрос
Ответил сок111213
0
<АСО = 90° (АС - касательная)
<АВО = 90° (АВ - касательная)
ОС = ОВ = 1/2 АО => <САО=<ОАВ=30°
<САВ = <САО+<ОАВ = 30°+30° = 60°
Ответ: <САВ = 60°
Приложения:
Ответил table123
0
Ответ:
Объяснение:
начерти окружность и из точки А проведи касательныеАС и АВ, т.О соедини с т.С и с т. В, и т.О с т. А, ОС перпендикулярна АС, ОВ перпендикулярна АВ по теор. о касательных и тогда тр-к ОСВ= тр-ку ОАВ по трем сторонам( ОС=ОВ=R, АС=АВ по теор о касательных, ОА- общая) и значит <CAO=<OAB.
Катет ОС=6, гипотенузаОА=12, т.е. ОС=1/2 ОА, и значит <CAO=30 гр., тогда <CAB=60гр.
Приложения:

Новые вопросы
Математика,
7 лет назад
История,
8 лет назад