ПОМОГИТЕ!!! ДАЮ 30 БАЛЛОВ!!!
На стороне ВС треугольника АВС выбрана точка О так, что ВО: ОС = 2: 3. В каком отношении медиана ВМ делит отрезок АО?

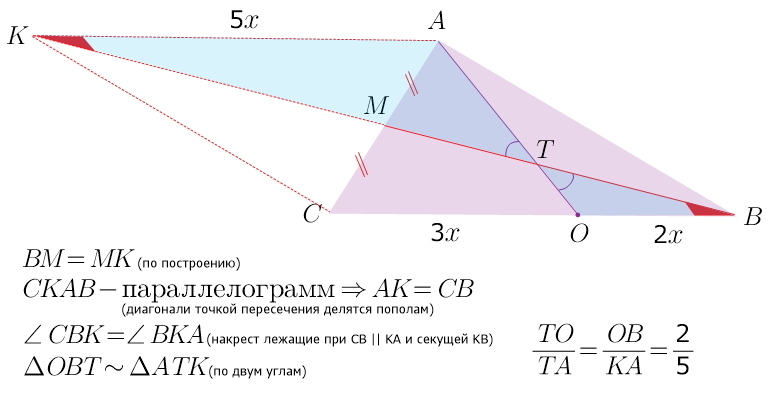
отрезок АО медианой делится в отношении 2:5

Вариант решения.

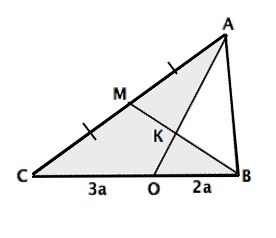
Рассмотрим треугольник САО. Медиана ВМ треугольника АВС пересекает сторону АС в точке М, К– точка её пересечения со стороной  АО, точка В – лежит на продолжении стороны СО. СМ=МА, ВО:ОС=2:3

Тогда, принимая во внимание отношение отрезков, на которые точки О и М делят ВС и АС, по теореме Менелая:

BС=ВО+ОС=5а

⇒ АК:КО=5:2