Алгебра, вопрос задал weteranartem43 , 11 месяцев назад

помогите дам 57 балов

Приложения:

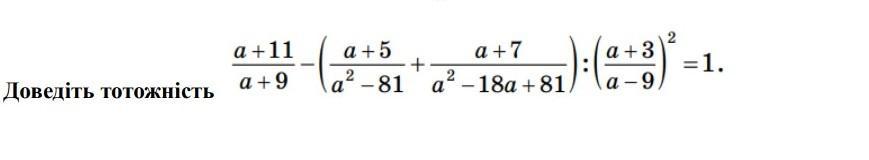
Ответы на вопрос

Ответил 7x8

1

Ответ:

$\displaystyle \frac{a+11}{a+9}-\left(\frac{a+5}{a^2-81}+\frac{a+7}{a^2-18a+81}\right):\left(\frac{a+3}{a-9}\right)^2=1$

Объяснение:

$\displaystyle \frac{a+11}{a+9}-\left(\frac{a+5}{a^2-81}+\frac{a+7}{a^2-18a+81}\right):\left(\frac{a+3}{a-9}\right)^2=\\\\\\\frac{a+11}{a+9}-\left(\frac{a+5}{(a-9)(a+9)}+\frac{a+7}{(a-9)^2}\right)\cdot\frac{(a-9)^2}{(a+3)^2}=\\\\\\\frac{a+11}{a+9}-\left(\frac{(a+5)(a-9)}{(a-9)^2(a+9)}+\frac{(a+7)(a+9)}{(a-9)^2(a+9)}\right)\cdot\frac{(a-9)^2}{(a+3)^2}=$

$\displaystyle\frac{a+11}{a+9}-\frac{a^2-9a+5a-45+a^2+9a+7a+63}{(a-9)^2(a+9)}\cdot\frac{(a-9)^2}{(a+3)^2}=\\\\\\\frac{a+11}{a+9}-\frac{2a^2 + 12a + 18}{a+9}\cdot\frac{1}{(a+3)^2}=\\\\\\\frac{a+11}{a+9}-\frac{2(a^2 + 6a + 9)}{a+9}\cdot\frac{1}{(a+3)^2}=$

$\displaystyle \frac{a+11}{a+9}-\frac{2(a+3)^2}{a+9}\cdot\frac{1}{(a+3)^2}=\\\\\\\frac{a+11}{a+9}-\frac{2}{a+9}=\frac{a+11-2}{a+9}=\frac{a+9}{a+9}=1$

weteranartem43: спс

7x8: :)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

География, 11 месяцев назад

Чем осуществляется Дистанционное зондирование?

Другие предметы, 11 месяцев назад

Як під готувати і відтягнути пораненого на спині? Опишіть дії стрільця-санітара, який, спостерігаючи за полем бою, побачив, що один з військовослужбовців отримав поранення правого стегна.

Українська мова, 11 месяцев назад

Даю 80 балів) зробіть все...

Математика, 11 месяцев назад

помогите пж 1.(2a-3b)(2a+3b)-3a² ,,,,,, 2.(5x-1)²+10x...

Литература, 6 лет назад

Литературное чтение на родном языке 4 класс произведенние Каффа нужно сделать 1-4 вопроса после текста.

Математика, 6 лет назад

3.Какие два числа надо вставить между числами 2 и - 543, чтобы они вместе с данными числами образовали геометрическую прогрессию?