Алгебра, вопрос задал ropenope361 , 6 лет назад

ПОМОГИТЕ АЛГЕбра сровно!!!!

Приложения:

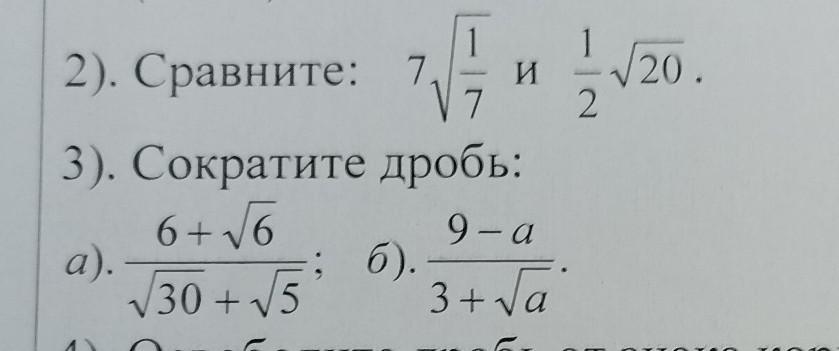
Simba2017: 2)7V(1/7)=V(49/7)=V7

Simba2017: 1/2V20=V(20/4)=V5

Simba2017: V7 больше V5

Ответы на вопрос

Ответил Аноним

2) Внесем под корень числа соответственно 7 и (1/2);

7√(1/7)=√(49/7)=√7; (1/2)√20=√(20/4)=√5, т.к функция у=√х возрастает на всей области определения, а именно при х ∈[0;+∞), и т.к. аргументы связаны с.о. 7>5, то √7>√5, значит, 7√(1/7)>(1/2)√20;

3) a) (6+√6)/(√30+√5)=(√6*(√6+1))/(√5*(√6+1))=√(6/5)=√1.2;

использовал 6=(√6)²; √30=√6*√5

б) (9-а)/(3+√а)=(3²-(√а)²)/(3+√а)=(3-√а)(3+√а)/(3+√а)=(3-√а)

использовал формулу а²-с²=(а-с)*(а+с);

Ответил NNNLLL54

Ответ:

$\boxed{\ a\sqrt{b}=\sqrt{a^2\cdot b}\ \ (a>0)\ \ ,\ \ \sqrt{a\cdot b}=\sqrt{a}\cdot \sqrt{b}\ \ ,\ \ a^2-b^2=(a-b)(a+b)\ }$

$2)\ \ 7\sqrt{\dfrac{1}{7}}=\sqrt{\dfrac{7^2}{7}}=\sqrt7\ \ ,\ \ \ \ \ \ \dfrac{1}{2}\sqrt{20}=\sqrt{\dfrac{1}{4}\cdot 20}=\sqrt5$

$y=\sqrt{x}$ - возрастающая функция, поэтому из того, что 7>5 следует,

неравенство $\sqrt{7}>\sqrt{5}$ . А значит $7\sqrt{\dfrac{1}{7}}>\dfrac{1}{2}\sqrt{20}$ .

$\displaystyle 3)\ \ \frac{6+\sqrt6}{\sqrt{30}+\sqrt5}=\frac{(\sqrt6)^2+\sqrt6}{\sqrt{6\cdot 5}+\sqrt5}=\frac{\sqrt6\cdot (\sqrt6+1)}{\sqrt5\cdot (\sqrt6+1)}=\frac{\sqrt6}{\sqrt5}=\sqrt{\frac{6}{5}}=\sqrt{1,2}$