Алгебра, вопрос задал svetlanaskackova905 , 6 лет назад

ПОМОГИ ПОЖАЛУЙСТА

найдите общий вид первообразных для функции y=f(x)​

Приложения:

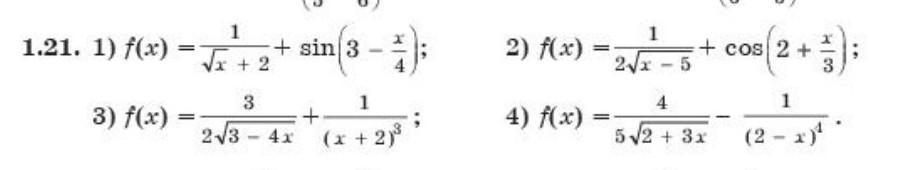
Ответы на вопрос

Ответил NNNLLL54
0

Ответ:

Пользуемся правилом интегрирования функции, зависящей от

линейной функции:  если   \displaystyle \int f(x)\, dx=F(x)+C  ,  то

 \displaystyle \int f(kx+b)\, dx=\frac{1}{k}\cdot F(kx+b)+C\ .

\displaystyle 1)\ \ F(x)=\int \frac{dx}{\sqrt{x}+2}+\int sin(3-\frac{x}{4})\, dx=\Big[\ \sqrt{x}=t\ ,\ x=t^2\ ,\ dx=2t\, dt\ \Big]=\\\\\\=\int \frac{2t\, dt}{t+2}-(-4)\cdot cos(3-\frac{x}{4})=2\int \Big(1-\frac{2}{t+2}\Big)\, dt+4\, cos(3-\frac{x}{4})=\\\\\\=2(t-2\, ln|t+2|)+4cos(3-\frac{x}{4})+C=\\\\=2(\sqrt{x} -2\, ln(\sqrt{x} +2))+4cos(3-\frac{x}{4})+C

Возможно, судя по остальным примерам,  корень был над всем выражением (х+2) , тогда  

\displaystyle F(x)=\int \frac{dx}{\sqrt{x+2}}+\int sin(3-\frac{x}{4})\, dx=2\sqrt{x+2}+4\, cos(3-\frac{x}{4})+C

\displaystyle 2)\ \ F(x)=\int \frac{dx}{2\sqrt{x-5}}+\int cos(2+\frac{x}{3})\, dx=\sqrt{x-5}+3sin(2+\frac{x}{3})+C\\\\\\3)\ \ F(x)=\int \frac{3\, dx}{2\sqrt{3-4x}}+\int \frac{dx}{(x+2)^3}=3\cdot \frac{1}{-4}\, \sqrt{3-4x}+\frac{(x+2)^{-2}}{-2}+C=\\\\\\=-\frac{3}{4}\, \sqrt{3-4x}+\frac{1}{2(x+2)^2}+C

4)\ \ \displaystyle F(x)=\int \frac{4}{5\sqrt{2+3x}}-\int \frac{dx}{(2-x)^4}=\frac{4}{5}\cdot 2\sqrt{2+3x}-\frac{(2-x)^{-3}}{-3}+C=\\\\\\=\frac{8}{5}\cdot \sqrt{2+3x}+\frac{1}{3(2-x)^3}+C

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык, 1 год назад
ребят? помогите пожалуйста!!! ме нужно написать рецензию на мою любимую книгу...я ничего не понимаю!!!
Русский язык, 1 год назад
Разбери по членам предложеня.Утром мы с дедушкой совершаем обход лесных владений...
История, 6 лет назад
почему съезд князей в Дмитрове сыграл важную роль в судьбе Москвы???​
Информатика, 6 лет назад
Написать программу которая вычисляет 1!*2!*3!*...*N!
Литература, 8 лет назад
что вы узнали о судьбах Падчерицы и Салдата из их диалога...
Алгебра, 8 лет назад
Пожалуйста помогите! Геометрическая прогрессия, 9 класс. За лучший ответ 50 баллов!!!