Алгебра, вопрос задал Goscharskiy , 6 лет назад

Помните прошу 30 балов

Приложения:

Ответы на вопрос

Ответил kotofeevicholeg

Ответ: 0

Решение:

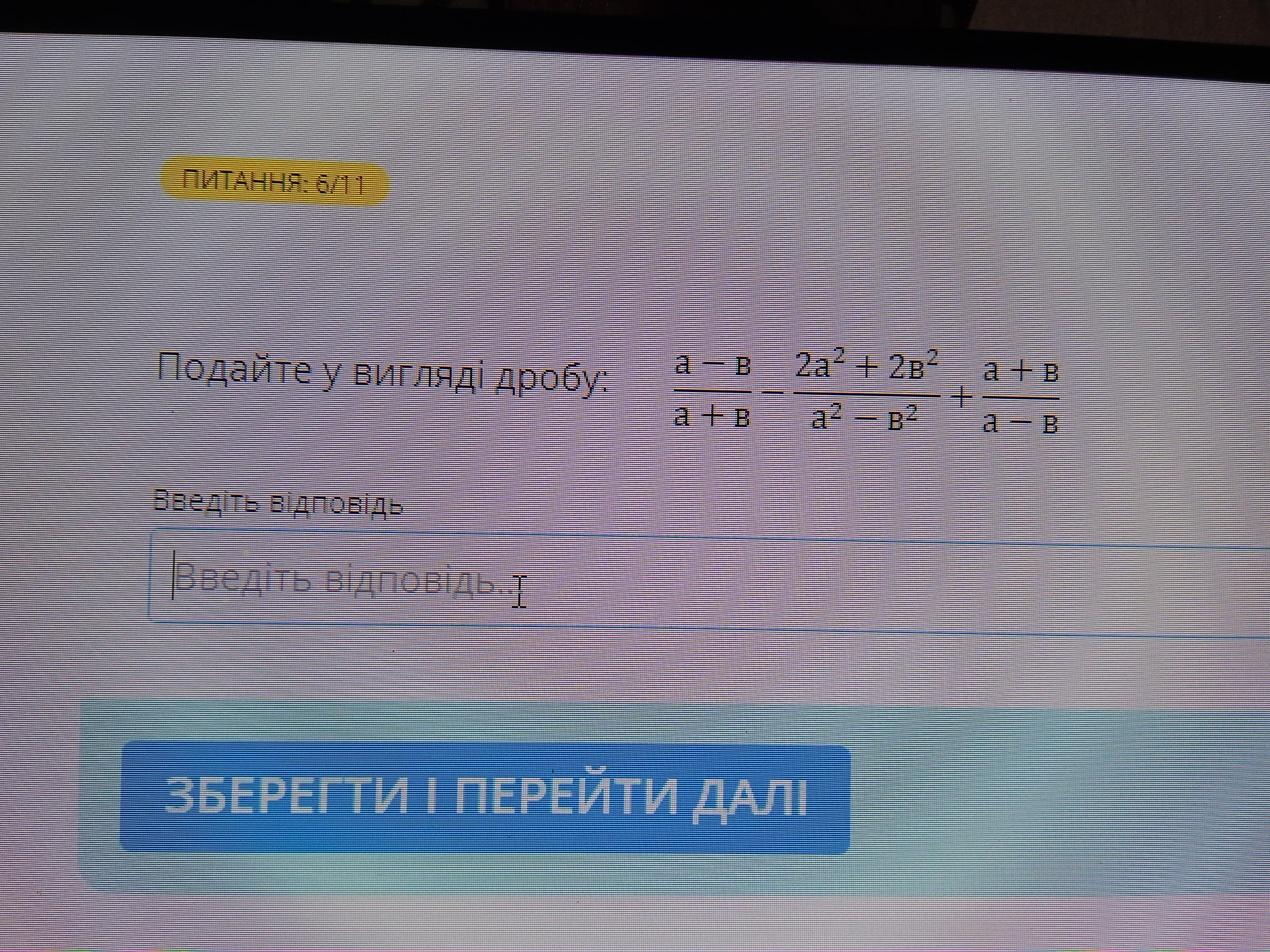
$\frac{a - b}{a + b} - \frac{2a^2 + 2b^2}{a^2-b^2} + \frac{a + b}{a-b} =$

Домножим 1ю дробь на (a - b), а 3ю на (a + b)

$\frac{(a^2 - 2ab + b^2)- (2a^2+2b^2) + (a^2 + 2ab + b^2)}{a^2-b^2} =\frac{a^2 - 2ab + b^2- 2a^2-2b^2 +a^2 + 2ab + b^2}{a^2-b^2} = \frac{0}{a^2 - b^2} = 0$

Ответил sailcar100

Ответ:

Объяснение:

$\frac{a-b}{a+b}-\frac{2a^{2}+2b^{2} }{a^{2}-b^{2} }+\frac{a+b}{a-b}=\\\\=\frac{(a-b)(a-b)-2a^{2}-2b^{2}+(a+b)(a+b)}{a^{2}-b^{2}}=\\\\=\frac{a^{2}-2ab+b^{2}-2a^{2}-2b^{2}+a^{2}+2ab+b^{2} }{a^{2}-b^{2}}=\\\\$

после приведения подобных, в числителе получится нуль, так как все слагаемые с противоположными знаками.

при делении нуля на любое число - получаем нуль

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

Множество всех первообразных функции y=-sinx+x²-4 имеет вид?

Биология, 1 год назад

ОЧЕНЬ СРОЧНО!!! Назовите основные признаки растений. Какое значение имеют растения в природе и жизни человека?

Математика, 6 лет назад

Виконуйте в метрах 3/5 км +8 1/3м-8дм...

Информатика, 6 лет назад

СРООООЧНО НА ПИТОНЕ 40 баллов Сдать решение задачи 6-Странное устройство Полный балл: 100 Ограничение времени: 1 с Ограничение памяти: 512M Ограничение размера стека: 64M Задача 6:...

Математика, 8 лет назад

из города выехал грузовик через 4 часа когда он проехал 168 км Из этого же города в том же направлении выехал Мотоциклист и догнал грузовик на расстоянии 420 км от города Найдите скорости грузовика и...

Литература, 8 лет назад

Тема рассказа что любит мишка...