Помагите СРОЧНО даю 20 балов
Приложения:

Ответы на вопрос
Ответил Rarit
0
#1
1. Верно. Ведь если треугольник равнобедренный, то тупой угол не может быть при основании, ведь в равнобедренном треугольнике углы при основании равны, значит сумма углов превысит 180°. Тогда тупой угол будет лежать против основания. Всем известно, что в тупоугольном треугольнике только один угол тупой, а остальные острые. Тогда основание будет лежать против большего угла, а против большего угла лежит большая сторона, значит основание больше боковых сторон.
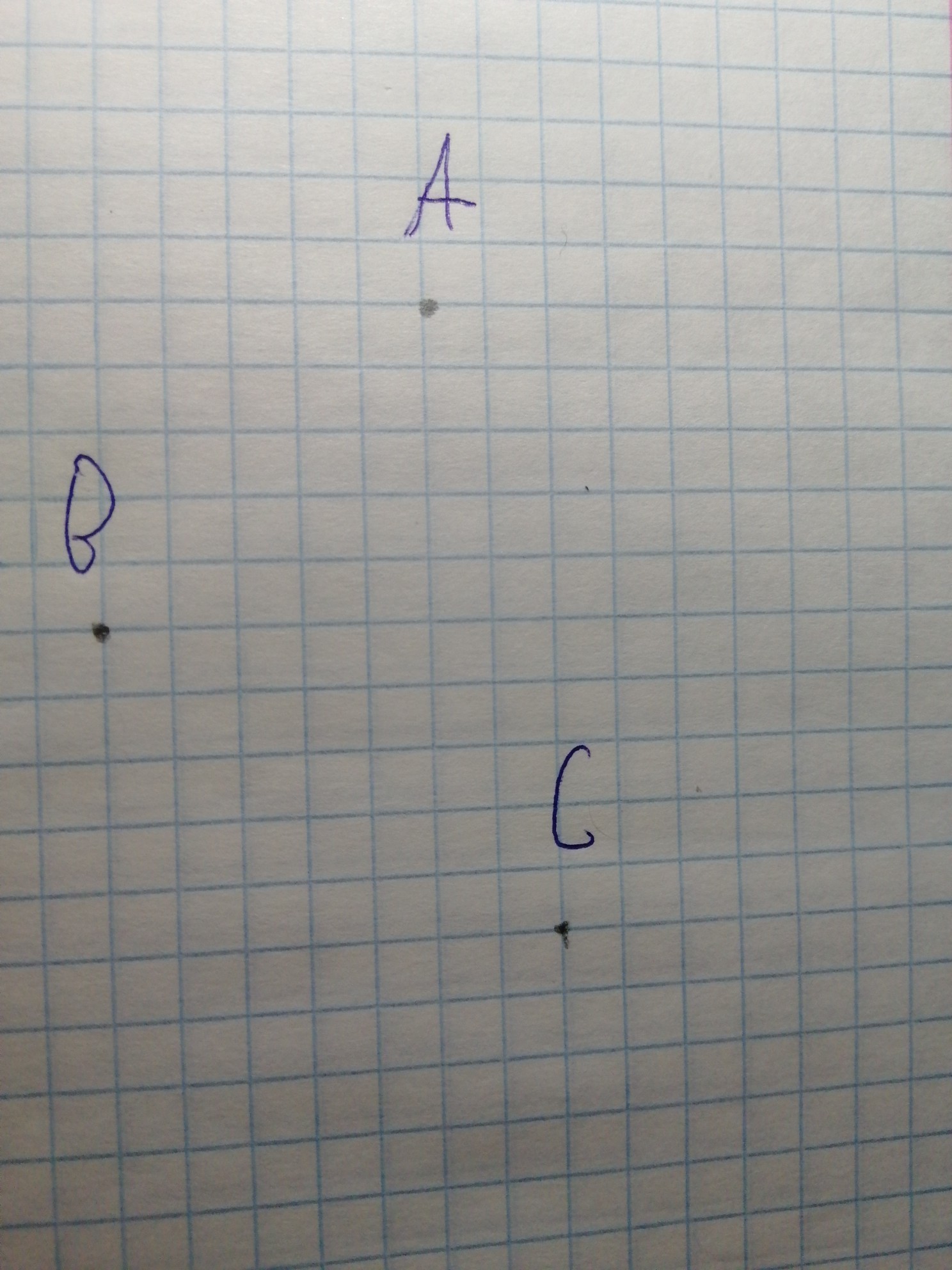
2. Не всегда. Если точки лежат на одной прямой, то утверждение верно, если же точки расположены так, как на первом фото, то есть они не лежат на одной прямой, то через них вообще не проходит какая-то прямая. В условии подразумевают любые три точки, значит утверждение неверно.
3. Не всегда. Они могут быть равны только тогда, когда третья прямая будет перпендикулярна по отношению к параллельным прямым. Но если прямая не будет перпендикулярна, то они равны не будут. А вообще если две параллельные прямые пересечены секущей, то сумма односторонних углов всегда равна 180°, но вопрос не об этом, значит утверждение снова неверно.
4. Не всегда. Соответственные углы должны быть равны между собой, чтобы прямые были параллельны. Если их сумма равна 180°, то они могут быть равны, только если секущая перпендикулярна к двум параллельным прямым, то есть не всегда они равны, значит утверждение опять неверно.
Ответ: только 1.
#2.
Допустим, что внешний угол при основании, тогда углы при основании равны 40°, ведь они равны, так как треугольник равнобедренный, а сумма внешнего угла и смежного с ним внутреннего угла треугольника равна 180°. Сумма всех углов треугольника равна 180°, два угла равны 40°, значит третий равен 100°.
Допустим, что внешний угол не при основании, тогда угол лежащий против основания равен 40°, а на оставшиеся углы приходится по 140°, а они равны, ведь они при основании, значит они оба равны 70°.
Ответ: 40°; 40°; 100° или 40°; 70°: 70°, смотря из ситуации.
#3.
Решение на фотографиях, извиняюсь за почерк. Если кратко, то необходимо построить треугольник, равный данному, затем доказать, что все стороны большого треугольника, состоящего из двух построенных, равны. Дальше необходимо доказать, что катет, лежащий на против угла в 30° данного треугольника, равен половине одной стороне большого. А так как в большом треугольнике, как мы убедились, все стороны, равны, то катет равен половине всем его сторонам, но по построению большого треугольника одна из его сторон – гипотенузе изначального маленького треугольника. Значит катет равен и её половине, что и требовалось доказать.
1. Верно. Ведь если треугольник равнобедренный, то тупой угол не может быть при основании, ведь в равнобедренном треугольнике углы при основании равны, значит сумма углов превысит 180°. Тогда тупой угол будет лежать против основания. Всем известно, что в тупоугольном треугольнике только один угол тупой, а остальные острые. Тогда основание будет лежать против большего угла, а против большего угла лежит большая сторона, значит основание больше боковых сторон.
2. Не всегда. Если точки лежат на одной прямой, то утверждение верно, если же точки расположены так, как на первом фото, то есть они не лежат на одной прямой, то через них вообще не проходит какая-то прямая. В условии подразумевают любые три точки, значит утверждение неверно.
3. Не всегда. Они могут быть равны только тогда, когда третья прямая будет перпендикулярна по отношению к параллельным прямым. Но если прямая не будет перпендикулярна, то они равны не будут. А вообще если две параллельные прямые пересечены секущей, то сумма односторонних углов всегда равна 180°, но вопрос не об этом, значит утверждение снова неверно.
4. Не всегда. Соответственные углы должны быть равны между собой, чтобы прямые были параллельны. Если их сумма равна 180°, то они могут быть равны, только если секущая перпендикулярна к двум параллельным прямым, то есть не всегда они равны, значит утверждение опять неверно.
Ответ: только 1.
#2.
Допустим, что внешний угол при основании, тогда углы при основании равны 40°, ведь они равны, так как треугольник равнобедренный, а сумма внешнего угла и смежного с ним внутреннего угла треугольника равна 180°. Сумма всех углов треугольника равна 180°, два угла равны 40°, значит третий равен 100°.
Допустим, что внешний угол не при основании, тогда угол лежащий против основания равен 40°, а на оставшиеся углы приходится по 140°, а они равны, ведь они при основании, значит они оба равны 70°.
Ответ: 40°; 40°; 100° или 40°; 70°: 70°, смотря из ситуации.
#3.
Решение на фотографиях, извиняюсь за почерк. Если кратко, то необходимо построить треугольник, равный данному, затем доказать, что все стороны большого треугольника, состоящего из двух построенных, равны. Дальше необходимо доказать, что катет, лежащий на против угла в 30° данного треугольника, равен половине одной стороне большого. А так как в большом треугольнике, как мы убедились, все стороны, равны, то катет равен половине всем его сторонам, но по построению большого треугольника одна из его сторон – гипотенузе изначального маленького треугольника. Значит катет равен и её половине, что и требовалось доказать.
Приложения:


Новые вопросы
Другие предметы,
1 год назад
Другие предметы,
1 год назад
Алгебра,
7 лет назад
Математика,
7 лет назад