Алгебра, вопрос задал vlad3996 , 9 лет назад

Показательное уравнение

Приложения:

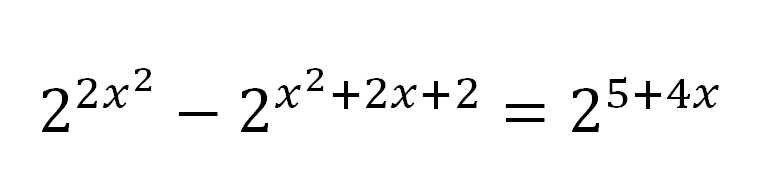
Ответы на вопрос

Ответил miad

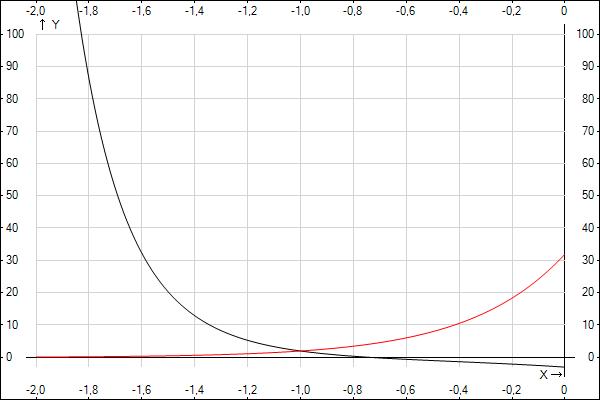
Ответом будет -1

Решение получил графически (черный - график левой части, а красный - правой)

Справа находится показательная функция и ее значение является положительным, тогда положительной должна быть и левая часть. Но это может быть только если:

$2x^2>x^2-2x-2$

Получаем $x^2-2x-2>0$

Приравниваем к нулю и находим дискриминант D=4-4*(-2)=12

Тогда корни $1pmsqrt{3}$

Т.к. коэффициент при $x^2$ 1>0, то ветви параболы идут вверх и решением данного неравенства будут интервалы $(-infty;1-sqrt{3})cup(1+sqrt{3};+infty)$

Это и есть область определения.

Далее можно сделать так:

$2^{2x^2}=2^{4x+5}+2^{x^2+2x+2}$

Теперь разделим правую и левую части на левое выражение:

$2^{0}=2^{-2x^2+4x+5}+2^{-x^2+2x+2}$

Здесь вот пока пробел в обосновании того, что правая часть может быть равна единице только тогда, когда оба слагаемых равны (т.е. они должны быть по 0,5, а это $2^{-1}$ )