Математика, вопрос задал gurlebaus00 , 7 лет назад

Показать, что функция y=ln2x удовлетворяет уравнению

Приложения:

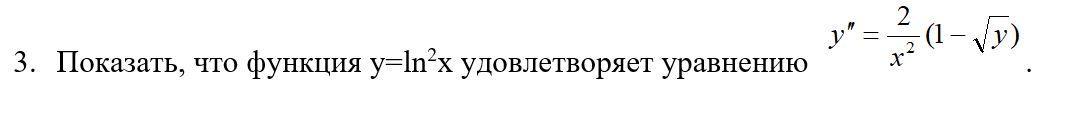
Ответы на вопрос

Ответил TheEvilGenius

$y = ln^2x\y' = (ln^2x)' = frac{2lnx}{x}\y'' = (frac{2lnx}{x})' = frac{(2lnx)'x - 2lnx(x)'}{x^2} = frac{2 - 2lnx}{x^2}\frac{2 - 2lnx}{x^2} = frac{2}{x^{2}} - frac{2lnx}{x^2} = frac{2}{x^{2}}(1 - lnx) =>\=> y'' = frac{2}{x^{2}}(1 - lnx)\$

Но y = ln²x => √y = lnx. Подставляем, получаем:

$y'' = frac{2}{x^{2}}(1 - sqrt{y})$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

проверочное слово опасно...

Русский язык, 1 год назад

прочетайте.найдите в приложении определения продолжыте описание погоды.подчеркните в вашем рассказе опредиления.Вчера светило яркое солнышка.Дал слабый,тёплый ветерок.Сегодня...помагите зделать...

Алгебра, 7 лет назад

С объяснением решения!

Математика, 7 лет назад

20 поділити на 0,6 яка відповідь...

Математика, 8 лет назад

черепаха за 3 мин может проползти 15 м, а слон за это же время пройдёт 300м. Какое расстояние может пройти каждый за 1 ч...

Математика, 8 лет назад

в гостиницу приехали 100 туристов из них 10 человек не знали немецкого и французского 75 туристов знали немецкий язык и 83 туристов знали французский язык сколько туристов знали оба языка французский...