Подскажите как решать подобные примеры, то, что в знаменателе получается 2^16+2^16+2^16+2^16 для меня понятно. Но как складывать степени с одинаковыми основаниями и показателями? Слышал, что нужно выводить общий множитель за скобки, но так ничего и не понял. Объясните поподробнее пожалуйста.
Приложения:
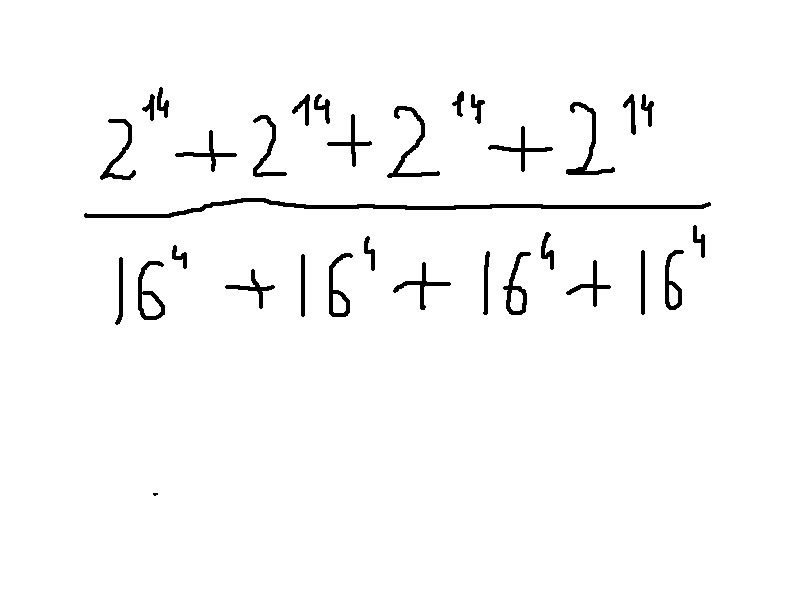
Ответы на вопрос
Ответил andrisd
0
andrisd:
Ошибка, сейчас исправлю.
1/4 получиться? 4 это 2^2 * 2^14 = 2^16 в знаменателе соответственно 2^16 Ответ 2^-2 =1/4
Понятно, где ваша ошибка. 16 - это не 2^4 а 2^3 и тогда (2^3)^4 = 2^(3·4) = 2^12
Запутали меня эти двоики, конехно же 16 = 2^4
Ответил 3NoTrumps
0
Вспомните, что такое число в степени - это одно и то же число умноженное на себя какое-то число раз. Тут вас просто сбивает то, что все - двойки и в конечном итоге получится добавление степени двойки и будет казаться, что это что-то непонятное.
По простому: а^3 + а^3 + а^3 + а^3 = ааа+ааа+ааа+ааа = ааа(1+1+1+1)=4ааа=4а^3
С вашими двоиками получится та же история..
По вышеописанному способу в числителе получится
2^14 + 2^14 + 2^14 + 2^14 = 4·2^14 = 2^16
В знаменателе - смотрим на одно из слагаемых
16^4 = (2·2·2·2)^4 = 2^(4·4)=2^16
т.е. 16^4 + 16^4 + 16^4 + 16^4 =4·16^4=4·2^16=2^18

По простому: а^3 + а^3 + а^3 + а^3 = ааа+ааа+ааа+ааа = ааа(1+1+1+1)=4ааа=4а^3
С вашими двоиками получится та же история..
По вышеописанному способу в числителе получится
2^14 + 2^14 + 2^14 + 2^14 = 4·2^14 = 2^16
В знаменателе - смотрим на одно из слагаемых
16^4 = (2·2·2·2)^4 = 2^(4·4)=2^16
т.е. 16^4 + 16^4 + 16^4 + 16^4 =4·16^4=4·2^16=2^18
ошиблись немного
Сейчас гляну. Тяжело, когда модератор постоянно удаляет написанное, но сам пишет с ошибками.
В знаменателе 2^18 еще одну двойку забыли и того ответ 2 в минус второй степени 1/4 поправьте, если я не прав.
Ошибаются все. А что касается Вашего первого решения, то оно было неполным. Такие решения удаляются, даже если и ответ верный.
16^4=2^3·2^3·2^3·2^3=2^12 и их четыре штуки, т.е. степень 12 + 2 - будет четырнадцатая.
На счет первого варианта - которое удаленное - так оно было опубликовано до того как картинка появилась. Уж не знаю почему так получилось. Грузилось в базу долго?!? (я всего лишь к тому, что писать по новой дольше, чем дописать или поправить)
А на счет знаменателя, попробуем по определению 16^4=8·8·8·8=2·2·2·2·2·2·2·2·2·2·2·2
Считаем количество двоек -12, т.е. =2^12
А на счет знаменателя, попробуем по определению 16^4=8·8·8·8=2·2·2·2·2·2·2·2·2·2·2·2
Считаем количество двоек -12, т.е. =2^12
Запутали меня эти двоики, да, там еще четыре 2ки и степень 16ая
Новые вопросы
Математика,
1 год назад
Русский язык,
1 год назад
Алгебра,
1 год назад
Математика,
1 год назад
Алгебра,
7 лет назад