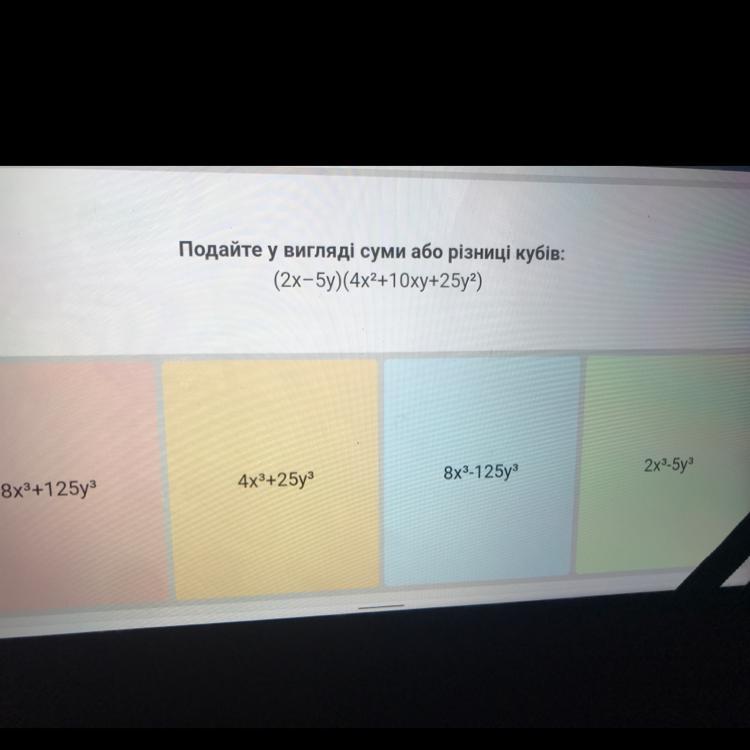
Подайте у вигляді суми або різниці кубів:
(2x-5y)(4x2+10xy+25y2)

Ответ:

Для множення двох багаточленів ми можемо використовувати формулу розкладу на множники:

(a - b)(a^2 + ab + b^2) = a^3 - b^3

Тому:

(2x - 5y)(4x^2 + 10xy + 25y^2)

= (2x)^3 - (5y)^3 + 2x*(-5y)(2x+5y)

= 8x^3 - 125y^3 - 10x^2y + 50xy^2

Отже, ми можем записати поданий вираз у вигляді суми кубів та добутку:

(2x - 5y)(4x^2 + 10xy + 25y^2) = 8x^3 - 125y^3 - 10x^2y + 50xy^2

або у вигляді різниці кубів:

(2x - 5y)(4x^2 + 10xy + 25y^2) = (2x)^3 - (5y)^3 - 3(2x)(5y)(2x-5y) = 8x^3 - 125y^3 - 30x^2y + 75xy^2