Побудуйте прямокутний трикутник за катетом і сумою гіпотенузи і другого катета .

Народ, потрібна ваша допомга, даю 50 балів) Дякую.

Ответ:

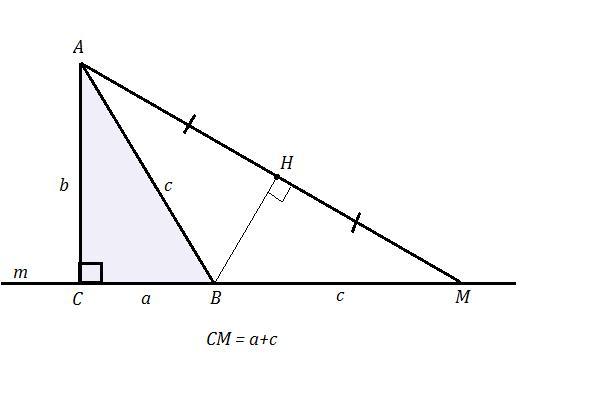
Рассмотрим прямоугольный треугольник АВС с катетами  a , b  и гипотенузой  с .

 Если продлим катет ВС на длину гипотенузы , то получим отрезок СМ , длиной равный сумме катета а и гипотенузы с :  СМ = a + c .

Тогда ΔАВМ будет равнобедренным , так как  АВ = ВМ .

Если провести в равнобедренном треугольнике АВМ высоту из вершины В , то её основание , точка Н , будет серединой стороны АМ , так как высота ВН является в равнобедренном треугольнике ещё и медианой , АН = МН .

Построение прямоугольного треугольника по катету b и сумме второго катета и гипотенузы  a+c .

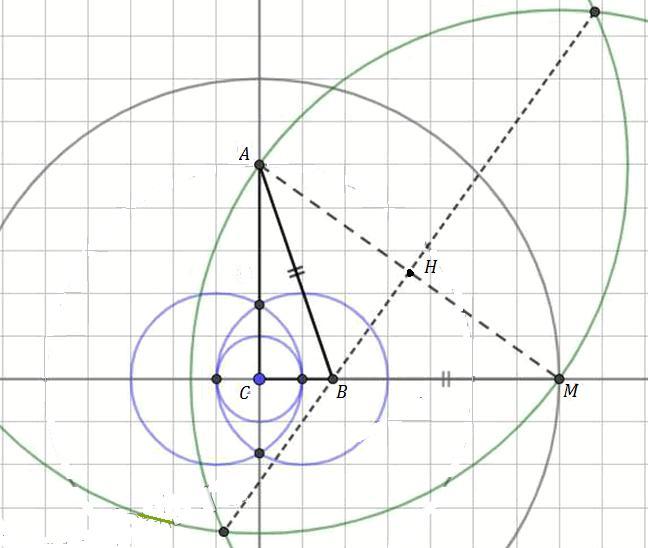
Сначала проводим произвольную прямую m , отмечаем на ней точку С и проводим  перпендикуляр СА . Для этого из точки С проведём окружность произвольного радиуса ,  отметим точки пересечения этой окружности с прямой m . Из точек пересечения , как из центров, проводим две окружности того же радиуса . Получим  две точки пересечения на первой окружности , соединим их прямой . Это и будет перпендикуляр к прямой m , проходящий через точку С . ( Можно проводить не полные окружности, а делать засечки . )

На этом перпендикуляре отложим отрезок СА , равный длине катета b , CA = b . Получим точку А .

Затем отложим на прямой m от точки С отрезок, равный  а + с . Получим точку М  и отрезок СМ = а + с .

Соединим прямой точку М с точкой А  .

Затем построим серединный перпендикуляр к отрезку АМ . Для этого из точек А и М построим окружности радиуса АМ . Соединим точки пересечения этих окружностей прямой . Эта прямая и будет серединным перпендикуляром к АМ . Получим точки пересечения серединного перпендикуляра с АМ и СМ - точки Н и В .

Соединим точку В с точкой А , получим искомый треугольник АВС .