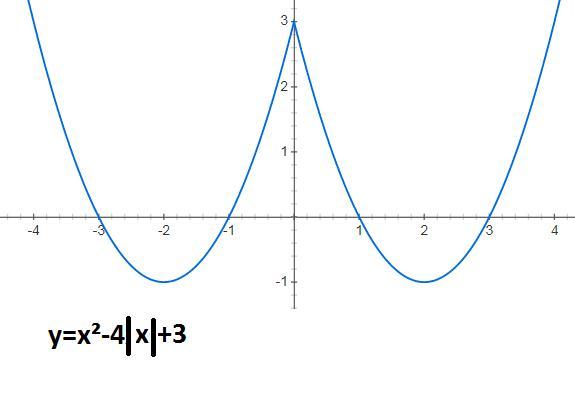
побудуйте графік функції y=x²-4|x|+3 використовуючи побудованою рафік укажіть найменше значення функції
Ответы на вопрос
Ответил bena20193
3
Ответ:
Объяснение:
y=x²-4|x|+3 = Ix²I-4|x|+3
это четная функция y(-x)=y(x)
график четной функции симметричен относительно оси ОУ.
Можно построить график для х>0 f а затем симметрично отобразить его относительно оси ОУ
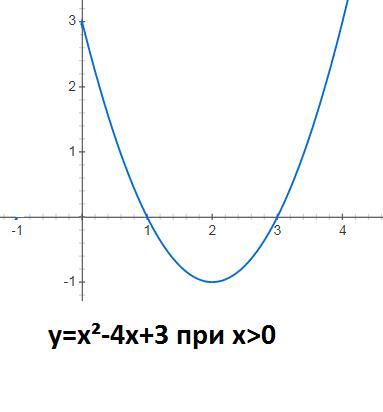
1) Построим график для х>0
при x>o IxI=x тогда y=x²-4|x|+3=x²-4x+3
y=x²-4x+3
это график квадратичной функции
вершина параболы х₀=-b/2a=4/2=2
y₀=y(2)=4-8+3=-1 (2;-1)
точка пересечения с осью ОУ х=0 у=3 (0;3)
точки пересечения с осью ОХ
у=0 x²-4x+3=0
x²-x-3x+3=x(x-1)-3(x-1)=(x-1)(x-3)=0
x₁=1 ; x2=3
(1;0) (3;0)
строим параболу при х>0
2) симметрично отображаем отображаем ее относительно оси ОУ
Приложения:
Новые вопросы
Английский язык,
1 год назад
Другие предметы,
1 год назад
Математика,
2 года назад
Математика,
2 года назад
Химия,
8 лет назад