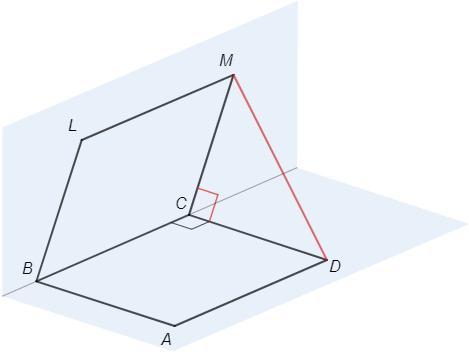
плоскости прямоугольника ABCD и параллелограмма BLMC перпендикулярны. Найдите длину отрезка MD, если DC=14см, BL=8√2см
​

В плоскости BMC проведем прямую СE⊥BC. ∠DCE - угол между плоскостями (угол между перпендикулярами к общей прямой). Плоскости перпендикулярны, ∠DCE - прямой. Прямая CD перпендикулярна двум прямым в плоскости (CD⊥BC, CD⊥CE), следовательно перпендикулярна плоскости, CD⊥BMC.

Доказали свойство:

Если прямая (CD), лежащая в одной из перпендикулярных плоскостей, перпендикулярна линии их пересечения (CD⊥BC), то она перпендикулярна другой плоскости (CD⊥BMC) и любой прямой в этой плоскости (CD⊥CM).

CM=BL=8√2 (противоположные стороны параллелограмма)

MD =√(CM^2 +CD^2) =√(128 +196) =18 см (т Пифагора)