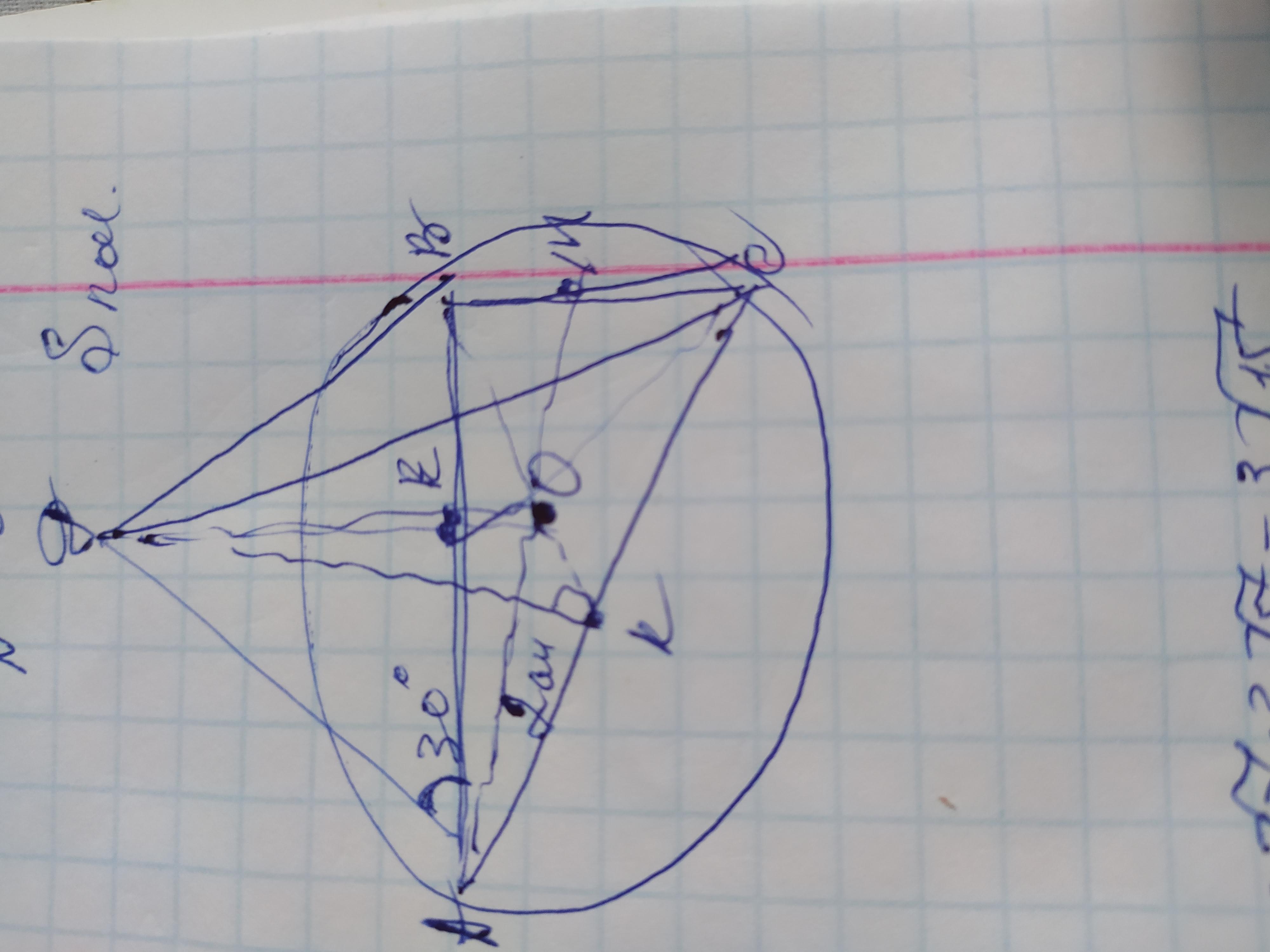
Плоскость боковой грани правильной треугольной пирамиды составляет угол 30 с плоскостью основания. Радиус окружности описанной около основания, равен 2см. Найти площадь полной поверхности пирамиды
Ответы на вопрос
Ответ: Sпол=40,2см²
Объяснение: обозначим вершины пирамиды АВСД с высотой ДО. В основании правильной 3 -угольной пирамиды лежит равносторонний треугольник. Рассмотрим ∆АДО. Он прямоугольный в котором АО и ДО - катеты, а АД- гипотенуза. < дАо=30°, а катет лежащий напротив него равен половине гипотенузы. Пусть катет ДО=х, тогда АД=2х. Составим уравнение используя теорему Пифагора:
(2х)²-х²=2²
4х²-х²=4
3х²=4
х²=4/3
х=√(4/3)=2/√3см, тогда АД=2√3×2=4√3см
Сторона "a"треугольника вписанного в окружность вычисляется по формуле радиуса: R=a/√3
a/√3=2
a=2√3
Стороны основания =2√3см
Площадь равносотороннего треугольника вычисляется по формуле:
Sосн=а²√3/4=
=(2√3)²×√3/4=4×3√3/4=3√3см²
Проведём апофему ДК и получим прямоугольный треугольник АДК, в котором АК и ДК - катеты, а АД- гипотенуза. ДК делит сторону АС пополам, поскольку боковая грань - это равнобедренный треугольник, поэтому АК=СК=2√3/2=√3см. Найдём ДК по теореме Пифагора:
ДК²=АД²-АК²=(4/√3)²-(√3)²=
=16×3-3=48-3=45; ДК=√45=3√5см
Найдём площадь боковой грани по формуле: S=½×AC×ДК=½×2√3×3√5=3√15см²
Таких граней 3, поэтому:
Sбок.пов=3√15×3=9√15см²
Sпол=Sосн+Sбок.пов=3√3+9√15=
=3×1,7+9×3,9=5,1+35,1=40,2см²