площадь треугольника,вершины которого совпадают с вершиной параболы y=x-1 и точками ее пересечения с осью абцисс
Ответы на вопрос
Ответил konrad509
0
Я предполагаю, что должно быть y=x²-1
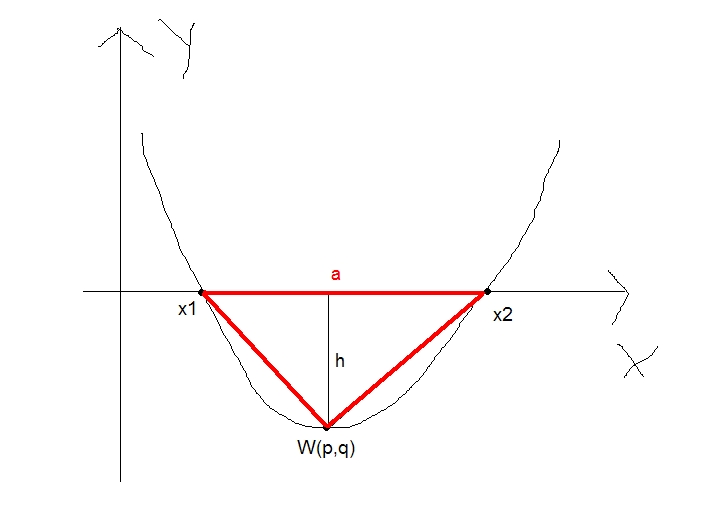
P=½ah
a=|x₁-x₂|
h=|q| (q - координат 'y' вершины параболы)
x²-1=0
(x-1)(x+1)=0
x₁=1, x₂=-1
a=|1-(-1)|
a=|1+1|
a=2
q=-Δ/4a
Δ=b²-4ac
a=1
b=0
c=-1
Δ=0²-4*1*(-1)
Δ=4
q=-4/(4*1)
q=-4/4
q=-1
h=|-1|
h=1
P=½*2*1
P=1
Рис вспомогательную в файлу.
---------------------------
Извините за мой русский ;)
Приложения:
Ответил vajny
0
Видимо в условии опечатка: парабола у = x^2 -1 (а не х-1).
Это стандартная парабола у = x^2, смещенная на 1 вниз по оси У.
Ее вершина, следовательно, расположена в т(0;-1).
Пересечения с осью Х:
x^2 -1 = 0 x^2 = 1 x1 = 1 x2 = -1
Площадь этого треугольника:
S = ah/2
Основание а - расстояние между х1 и х2: х1 - х2 = 2
Высота h - координата у вершины, взятая по модулю. h = 1
Тогда площадь:
S = 2*1/2 = 1
Ответ: 1.
Приложения:

Новые вопросы
Математика,
10 лет назад
Математика,
10 лет назад