Площадь кругового сектора равна 6π см^2, а радиус окружности - 4см. Найдите длину хорды, стягивающую дугу этого сектора
Приложения:
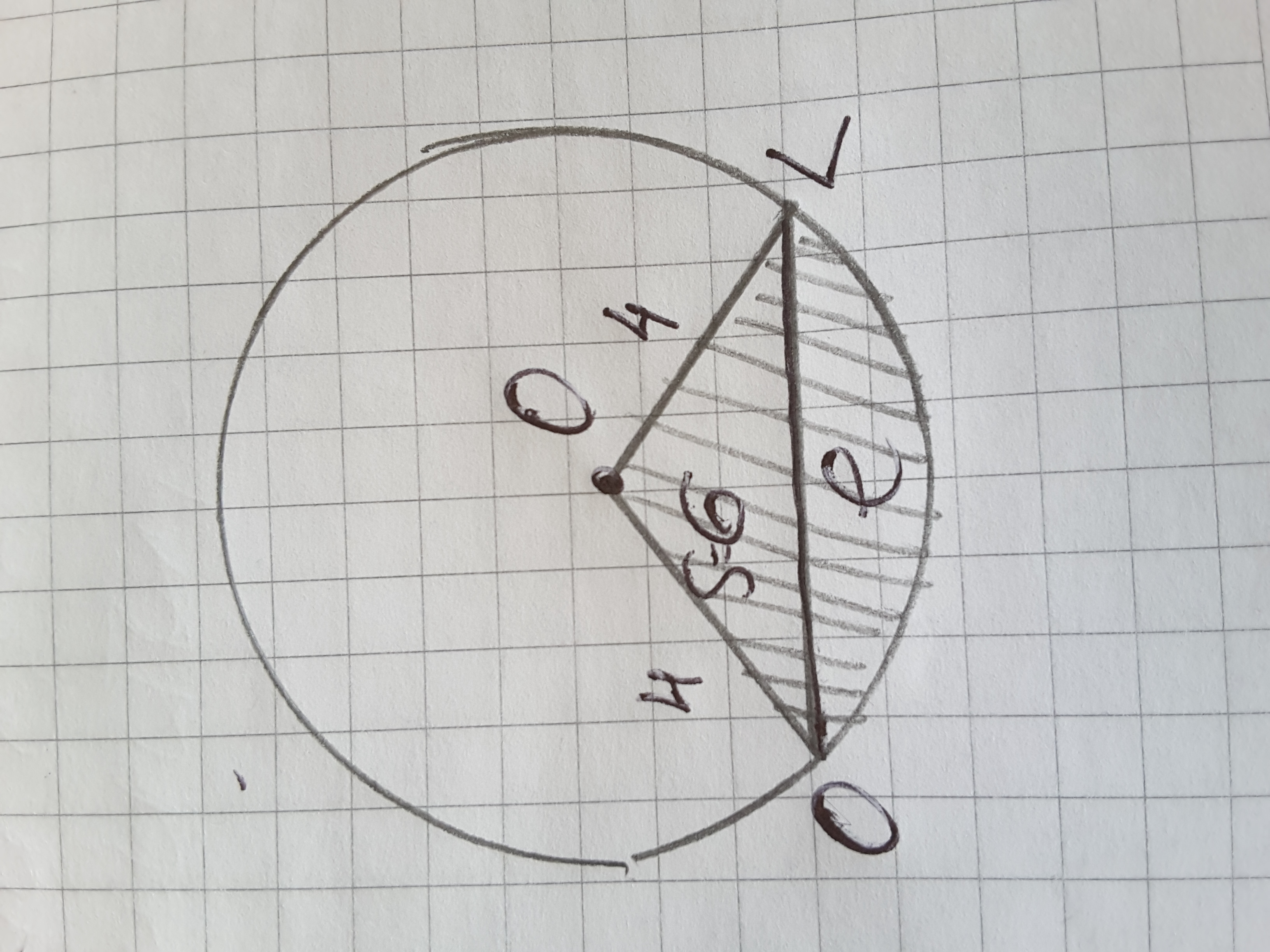
Ответы на вопрос
Ответил superdanielbro
26
Формула длины дуги сектора
т.е. длина окружности делится на ее градусную меру и умножается на величину угла сектора.
По условию •α=2π, откуда
Формула площади кругового сектора S=•α, т.е. площадь полного круга делится на его градусную меру и умножается на градусную меру сектора.
Подставим в формулу площади найденное из длины дуги значение R:
По условию π•360°/α=6π ⇒
α=60°⇒ R=360°:60°=6 см
Проведем биссектрису ОН угла сектора и к точке её пересечения с окружностью проведем касательную . Продлим стороны угла сектора до пересечения с касательной в т.А и В.
∆ АОВ - равносторонний с высотой ОН=R=6
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты.
r=6:3=2
C=2πr=4π
Новые вопросы