Плиз помогите сделать!!!!!!!!!
Приложения:
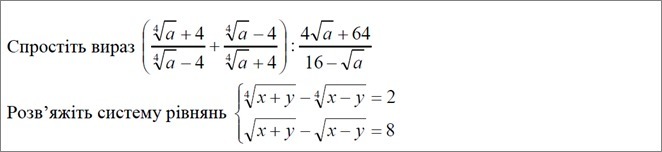
Ответы на вопрос
Ответил Удачник66
1
1) Упростить
![( \frac{ \sqrt[4]{a}+4}{\sqrt[4]{a}-4} + \frac{\sqrt[4]{a}-4}{\sqrt[4]{a}+4} ): \frac{4 \sqrt{a} +64}{16- \sqrt{a} } = \frac{(\sqrt[4]{a}+4)^2+(\sqrt[4]{a}-4)^2}{(\sqrt[4]{a}-4)(\sqrt[4]{a}+4)} * \frac{16- \sqrt{a} }{4 \sqrt{a} +64} =](https://tex.z-dn.net/?f=%28+%5Cfrac%7B+%5Csqrt%5B4%5D%7Ba%7D%2B4%7D%7B%5Csqrt%5B4%5D%7Ba%7D-4%7D+%2B+%5Cfrac%7B%5Csqrt%5B4%5D%7Ba%7D-4%7D%7B%5Csqrt%5B4%5D%7Ba%7D%2B4%7D+%29%3A+%5Cfrac%7B4+%5Csqrt%7Ba%7D+%2B64%7D%7B16-+%5Csqrt%7Ba%7D+%7D+%3D+%5Cfrac%7B%28%5Csqrt%5B4%5D%7Ba%7D%2B4%29%5E2%2B%28%5Csqrt%5B4%5D%7Ba%7D-4%29%5E2%7D%7B%28%5Csqrt%5B4%5D%7Ba%7D-4%29%28%5Csqrt%5B4%5D%7Ba%7D%2B4%29%7D+%2A+%5Cfrac%7B16-+%5Csqrt%7Ba%7D+%7D%7B4+%5Csqrt%7Ba%7D+%2B64%7D+%3D "( \frac{ \sqrt[4]{a}+4}{\sqrt[4]{a}-4} + \frac{\sqrt[4]{a}-4}{\sqrt[4]{a}+4} ): \frac{4 \sqrt{a} +64}{16- \sqrt{a} } = \frac{(\sqrt[4]{a}+4)^2+(\sqrt[4]{a}-4)^2}{(\sqrt[4]{a}-4)(\sqrt[4]{a}+4)} * \frac{16- \sqrt{a} }{4 \sqrt{a} +64} =")
![= \frac{ \sqrt{a} +2*4 \sqrt[4]{a} +16+\sqrt{a} -2*4 \sqrt[4]{a} +16}{ \sqrt{a} -16}* \frac{16- \sqrt{a} }{4 \sqrt{a} +64}=- \frac{2 \sqrt{a} +32}{4 \sqrt{a} +64}=- \frac{1}{2}](https://tex.z-dn.net/?f=%3D+%5Cfrac%7B+%5Csqrt%7Ba%7D+%2B2%2A4+%5Csqrt%5B4%5D%7Ba%7D+%2B16%2B%5Csqrt%7Ba%7D+-2%2A4+%5Csqrt%5B4%5D%7Ba%7D+%2B16%7D%7B+%5Csqrt%7Ba%7D+-16%7D%2A+%5Cfrac%7B16-+%5Csqrt%7Ba%7D+%7D%7B4+%5Csqrt%7Ba%7D+%2B64%7D%3D-+%5Cfrac%7B2+%5Csqrt%7Ba%7D+%2B32%7D%7B4+%5Csqrt%7Ba%7D+%2B64%7D%3D-+%5Cfrac%7B1%7D%7B2%7D+ "= \frac{ \sqrt{a} +2*4 \sqrt[4]{a} +16+\sqrt{a} -2*4 \sqrt[4]{a} +16}{ \sqrt{a} -16}* \frac{16- \sqrt{a} }{4 \sqrt{a} +64}=- \frac{2 \sqrt{a} +32}{4 \sqrt{a} +64}=- \frac{1}{2}")
2) Система
{![\sqrt[4]{x+y} - \sqrt[4]{x-y}=2](https://tex.z-dn.net/?f=+%5Csqrt%5B4%5D%7Bx%2By%7D+-+%5Csqrt%5B4%5D%7Bx-y%7D%3D2+ "\sqrt[4]{x+y} - \sqrt[4]{x-y}=2")
{
Замена![\sqrt[4]{x+y}=a; \sqrt[4]{x-y} =b](https://tex.z-dn.net/?f=+%5Csqrt%5B4%5D%7Bx%2By%7D%3Da%3B++%5Csqrt%5B4%5D%7Bx-y%7D+%3Db+ "\sqrt[4]{x+y}=a; \sqrt[4]{x-y} =b")
{ a - b = 2
{ a^2 - b^2 = 8
Разложим 2 уравнение на разность квадратов
{ a - b = 2
{ (a - b)(a + b) = 8
Делим 2 уравнение на 1 уравнение
{ a - b = 2
{ a + b = 4
Складываем уравнения
![2a=2+4=6; a= \sqrt[4]{x+y}=6/2 =3; x+y=3^4=81](https://tex.z-dn.net/?f=2a%3D2%2B4%3D6%3B+a%3D+%5Csqrt%5B4%5D%7Bx%2By%7D%3D6%2F2+%3D3%3B+x%2By%3D3%5E4%3D81 "2a=2+4=6; a= \sqrt[4]{x+y}=6/2 =3; x+y=3^4=81")
![b= \sqrt[4]{x-y} =4-a=4-3= 1;x-y=1^4=1](https://tex.z-dn.net/?f=b%3D+%5Csqrt%5B4%5D%7Bx-y%7D+%3D4-a%3D4-3%3D+1%3Bx-y%3D1%5E4%3D1 "b= \sqrt[4]{x-y} =4-a=4-3= 1;x-y=1^4=1")
Получаем новую систему
{ x + y = 81
{ x - y = 1
Складываем уравнения
2x = 82; x = 41
y = 81 - x = 81 - 41 = 40
2) Система
{
{
Замена
{ a - b = 2
{ a^2 - b^2 = 8
Разложим 2 уравнение на разность квадратов
{ a - b = 2
{ (a - b)(a + b) = 8
Делим 2 уравнение на 1 уравнение
{ a - b = 2
{ a + b = 4
Складываем уравнения
Получаем новую систему
{ x + y = 81
{ x - y = 1
Складываем уравнения
2x = 82; x = 41
y = 81 - x = 81 - 41 = 40
Новые вопросы