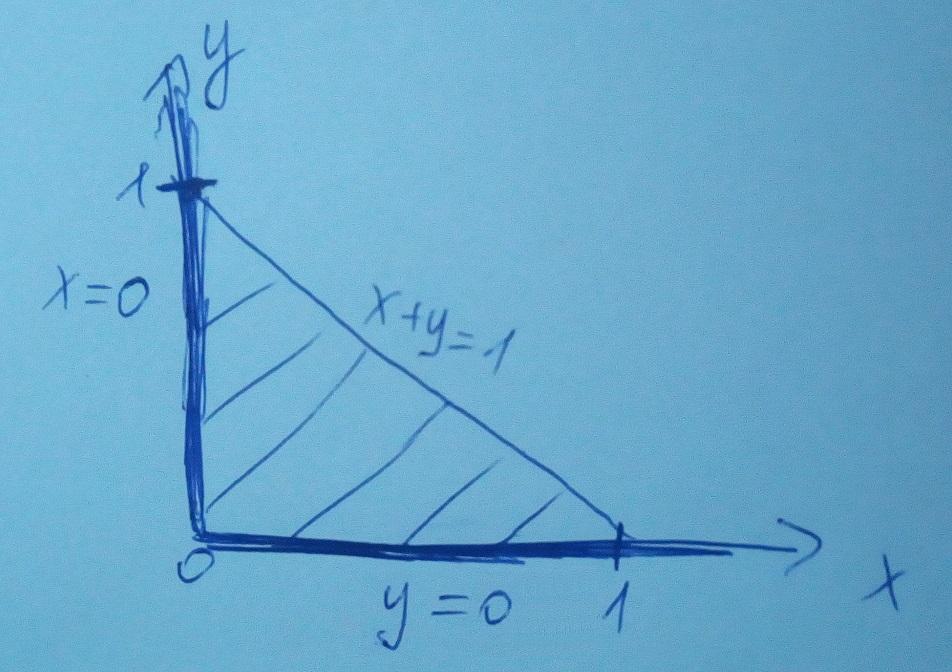
Алгебра, вопрос задал Santa2022 , 6 лет назад

пластина ограничена прямыми х+у=1, у=0, х=0
найти площадь фигуры, массу пластины, статические моменты относительно осей х и у
плотность задается уравнением плотность=у+3

Ответы на вопрос

Ответил Artem112

$0\leqslant x\leqslant 1;\ 0\leqslant y\leqslant 1-x$

Символом $\boxed{=}$ будем разрывать вычисление внешнего интеграла для вычисления внутреннего.

Площадь:

$S=\iint\limits_D dxdy=\int\limits^1_0dx \int\limits^{1-x}_0dy\ \boxed{=}$

$\int\limits^{1-x}_0dy=y|^{1-x}_0=(1-x)-0=1-x$

$\boxed{=}\int\limits^1_0(1-x)dx=\left.\left(x-\dfrac{x^2}{2} \right)\right|^1_0=\left(1-\dfrac{1^2}{2} \right)-\left(0-\dfrac{0^2}{2} \right)=1-\dfrac{1}{2}=\dfrac{1}{2}$

Масса:

$m=\iint\limits_D \rho(x;y)dxdy=\int\limits^1_0dx \int\limits^{1-x}_0(y+3)dy\ \boxed{=}$

$\int\limits^{1-x}_0(y+3)dy=\left.\left(\dfrac{y^2}{2}+3y\right)\right|^{1-x}_0=\left(\dfrac{(1-x)^2}{2}+3(1-x)\right)-\left(\dfrac{0^2}{2}+3\cdot0\right)=$

$=\left(\dfrac{1-2x+x^2}{2}+3-3x\right)-0=\dfrac{1}{2} -x+\dfrac{1}{2} x^2+3-3x=\dfrac{1}{2} x^2-4x+\dfrac{7}{2}$

$\boxed{=}\int\limits^1_0\left(\dfrac{1}{2} x^2-4x+\dfrac{7}{2}\right)dx=\left.\left(\dfrac{1}{2} \cdot\dfrac{x^3}{3} -4\cdot\dfrac{x^2}{2} +\dfrac{7}{2}x\right)\right|^1_0=$

$=\left(\dfrac{1}{2} \cdot\dfrac{1^3}{3} -4\cdot\dfrac{1^2}{2} +\dfrac{7}{2}\cdot1\right)-0=\dfrac{1}{6} -2+\dfrac{7}{2}=\dfrac{1-12+21}{6} =\dfrac{10}{6} =\dfrac{5}{3}$

Статический момент относительно оси х:

$M_x=\iint\limits_D y\rho(x;y)dxdy=\int\limits^1_0dx \int\limits^{1-x}_0y(y+3)dy\ \boxed{=}$

$\int\limits^{1-x}_0y(y+3)dy=\int\limits^{1-x}_0(y^2+3y)dy=\left.\left(\dfrac{y^3}{3}+\dfrac{3y^2}{2} \right)\right|^{1-x}_0=$

$=\left(\dfrac{(1-x)^3}{3}+\dfrac{3(1-x)^2}{2} \right)-0=\dfrac{1-3x+3x^2-x^3}{3}+\dfrac{3-6x+3x^2}{2}=$

$=\dfrac{1}{3}-x+x^2-\dfrac{1}{3}x^3+\dfrac{3}{2}-3x+\dfrac{3}{2}x^2=-\dfrac{1}{3}x^3+\dfrac{5}{2}x^2-4x+\dfrac{11}{6}$

$\boxed{=}\int\limits^1_0\left(-\dfrac{1}{3}x^3+\dfrac{5}{2}x^2-4x+\dfrac{11}{6}\right)dx =\left.\left(-\dfrac{1}{3}\cdot\dfrac{x^4}{4} +\dfrac{5}{2}\cdot\dfrac{x^3}{3} -4\cdot\dfrac{x^2}{2} +\dfrac{11}{6}x\right)\right|^1_0=$

$=\left(-\dfrac{1}{3}\cdot\dfrac{1^4}{4} +\dfrac{5}{2}\cdot\dfrac{1^3}{3} -4\cdot\dfrac{1^2}{2} +\dfrac{11}{6}\cdot1\right)-0=-\dfrac{1}{12} +\dfrac{5}{6} -2 +\dfrac{11}{6}=\dfrac{7}{12}$

Статический момент относительно оси y:

$M_y=\iint\limits_D x\rho(x;y)dxdy=\int\limits^1_0dx \int\limits^{1-x}_0x(y+3)dy\ \boxed{=}$

$\int\limits^{1-x}_0x(y+3)dy=x\int\limits^{1-x}_0(y+3)dy=x\left(\dfrac{1}{2} x^2-4x+\dfrac{7}{2}\right)=\dfrac{1}{2} x^3-4x^2+\dfrac{7}{2}x$

$\boxed{=}\int\limits^1_0\left(\dfrac{1}{2} x^3-4x^2+\dfrac{7}{2}x\right)dx=\left.\left(\dfrac{1}{2}\cdot\dfrac{x^4}{4} -4\cdot\dfrac{x^3}{3}+\dfrac{7}{2}\cdot\dfrac{x^2}{2}x\right)\right|^1_0=$

$=\left(\dfrac{1}{2} \cdot\dfrac{1^4}{4} -4\cdot\dfrac{1^3}{3} +\dfrac{7}{2}\cdot\dfrac{1^2}{2}\right)-0=\dfrac{1}{8} -\dfrac{4}{3} +\dfrac{7}{4}=\dfrac{13}{24}$