Первый вариант дифференциальные уравнения
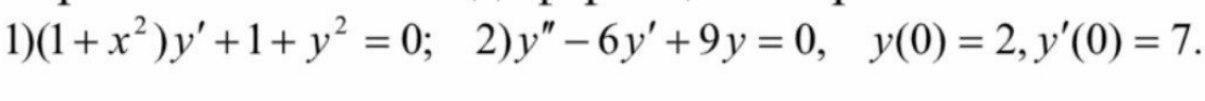
Ответы на вопрос
Ответ:
Диффер. ур-е с разделяющимися переменными .
ЛОДУ 2 пор.
Характеристическое уравнение
По виду корней характ. ур-я запишем вид общего решения ЛОДУ 2 порядка с постоянными коэффициентами .
Найдём частное решение . Используем начальные условия.
Частное решение: .
Отвечаю по Вашей просьбе
1. по условию дано уравнение с разделяющимися переменными
у'=dy/dx
разделим переменные, получим табличные интегралы.
-∫dx/(1+x²)=∫dy/(1+y²)
-arctgx+с=arctgy;
arctgx+arctgy=с- общий интеграл.
2. найдем корни характеристического уравнения
к²-6к+9=0; (к-3)²=0; к₁,₂=3 - двукратный действительный корень, поэтому общее решение однородного уравнения ищем в виде
у=c₁е³ˣ+х*с₂е³ˣ
чтобы найти коэффициенты с₁; с₂ найдем еще производную общего решения и подставим в функцию и ее производную начальные данные, получим
у=c₁е³ˣ+х*с₂е³ˣ
y'=3c₁e³ˣ+c₂e³ˣ+3xc₂e³ˣ
e⁰=1
_____________________
у(0)=c₁е⁰+0*с₂е⁰=2⇒c₁=2
y'(0)=3c₁e⁰+c₂e⁰+3*0e⁰=7⇒c₂=7-3*2=1
подставим в общее решение у=c₁е³ˣ+х*с₂е³ˣ найденные значения с₁ и с₂, получим частное решение данного уравнения
уч=2е³ˣ+х*е³ˣ