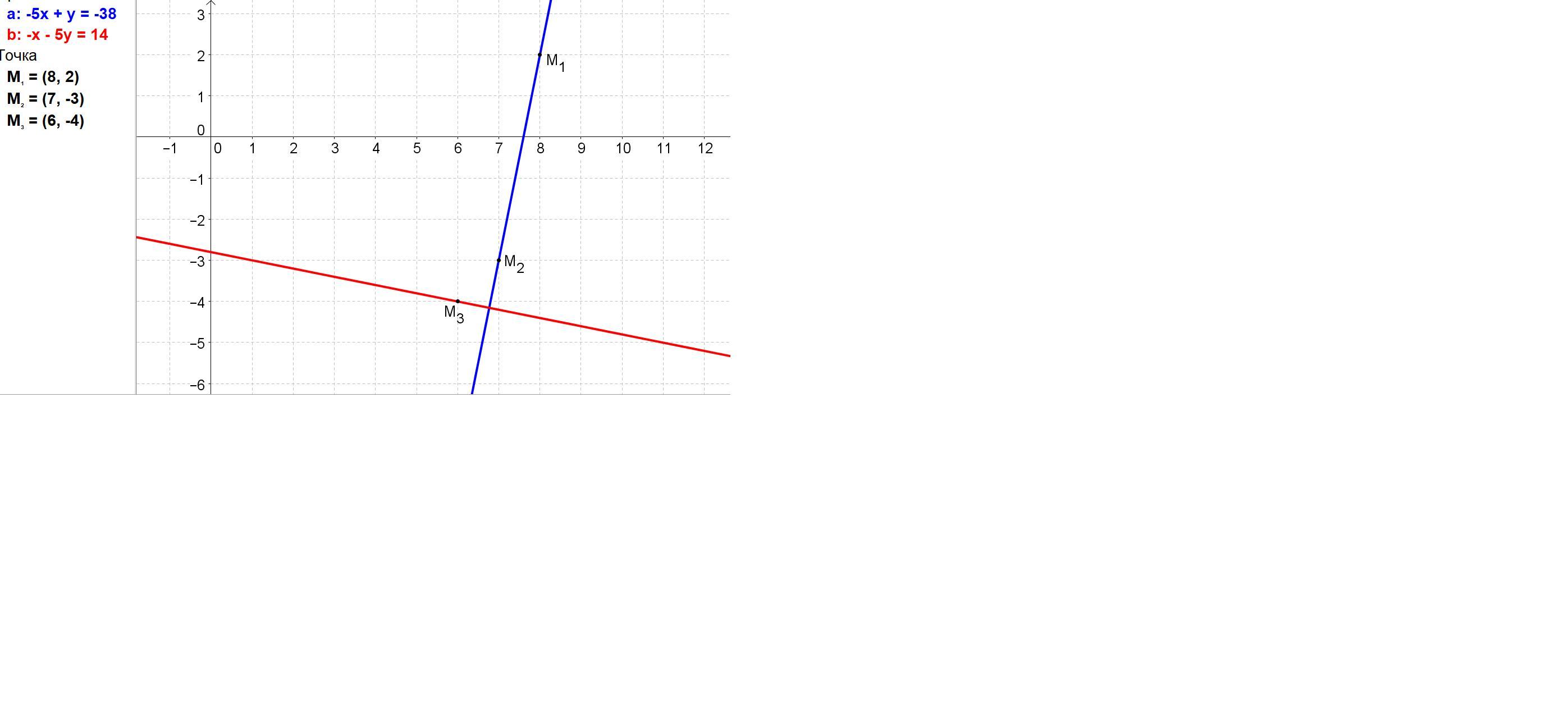
Перша пряма проходить через дві точки М 1*(8: 2) та М 2*(+7;:3). Друга, перпендикулярно перший, через точку М 3*(+6:-4). Написати рівняння прямих. Бал" Виконати креслення в системі координат

1)   5 3 4 6  

  3 1 1 1  

  4 -2 -1 1  

      5 3 4 5 3 -5 12 -24

3 1 1 3 1 -9 -10 16 -14 -14

4 -2 -1 4 -2    

6 3 4 6 3 -6 3 -8 Δ1 =

1 1 1 1 1 -3 -12 4 0 8,32667E-16

1 -2 -1 1 -2    

5 6 4 5 6 -5 24 12 Δ2 =

3 1 1 3 1 -18 5 16 28 28

4 1 -1 4 1    

5 3 6 5 3 5 12 -36 Δ3 =

3 1 1 3 1 9 -10 24 -42 -42

4 -2 1 4 -2    

х1 = 0/ -14 = 0      

х2 = 28/ -14 = -2      

х3 = -42/ -14 = 3    

2) Вектор М1М2 = ((7 – 8); (-3 – 2)) = (-1; -5).

Уравнение прямой М1М2:

(х – 8)/(-1) = (у – 2)/(-5) каноническое.

-5х + 40 = -у + 2,

5х – у – 38 = 0             общее в виде Ах + Ву + С = 0.

Для перпендикулярной прямой коэффициенты А и В меняются на В и (-А) или (-В) и А.

Уравнение перпендикулярной прямой:

х + 5у + С = 0.

Для определения величины С подставим координаты точки М3.

6 + 5*(-4) + С = 0, отсюда С = 20 – 6 = 14.

Уравнение перпендикулярной прямой:

х + 5у + 14 = 0.

3)  

   z = -3 + 12xy + 4x²y + 7y³ - 9y.

d(z)/d(x) = 12y + 8xy = 4y(3 + 2x),            

d(z)/d(y) = 12x + 4x² + 21y² - 9.        

Приравниваем нулю производные.

4у(3 + 2х) = 0, у = 0, х = -3/2.

12x + 4x² + 21y² - 9 = 0,

12*(-3/2) + 4*(-3/2)² + 21y² - 9 = 0,

-18 + 9 + 21y² - 9 = 0,

21y² = 18,

у = ±√(18/21) = ±√((6/7).

Находим значение функции при переменных х = (-3/2) и у = ±√(6/7).

z(max) = 12√(6/7) – 3 при х = (-3/2) и у = -√(6/7).  

z(min) = -12√(6/7) – 3 при х = (-3/2) и у = √(6/7).