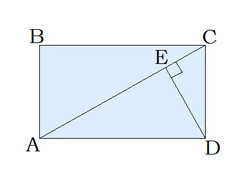
Перпендикуляр, который проведён из вершины прямоугольника к его диагонали, делит прямой угол в отношении 8 : 1.
Вычисли острый угол между диагоналями прямоугольника.
пожалуйста срочно!
Приложения:
Ответы на вопрос
Ответил KuOV
0
∠CDE составляет одну часть, ∠ADE - 8 таких частей, всего 9 частей.
∠CDE = 90° : 9 = 10°
Сумма острых углов прямоугольного треугольника 90°, тогда из ΔCDE:
∠DCE = 90° - ∠CDE = 90° - 10° = 80°
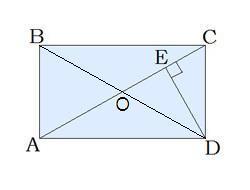
Диагонали прямоугольника равны и точкой пересечения делятся пополам, тогда ΔCOD равнобедренный (CO = OD), значит углы при его основании равны:
∠OCD = ∠ODC = 80°.
В ΔOCD находим третий угол:
∠COD = 180° - (∠OCD + ∠ODC) = 180° - 160° = 20° - угол между диагоналями.
Приложения:
Новые вопросы
Английский язык,
2 года назад
Физика,
2 года назад
Математика,
8 лет назад
Физика,
8 лет назад
Математика,
9 лет назад