Математика, вопрос задал xDanielAngelx , 2 года назад

P.S там где числа,сверху градус*

Приложения:

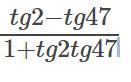
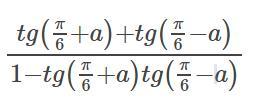
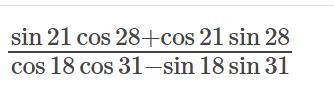
Ответы на вопрос

Ответил MatemaT123

Ответ:

$-1;$

$\sqrt{3};$

$tg49^{\circ};$

Пошаговое объяснение:

$tg2^{\circ}-tg47^{\circ}=\dfrac{sin(2^{\circ}-47^{\circ})}{cos2^{\circ} \cdot cos47^{\circ}}=\dfrac{sin(-45^{\circ})}{\dfrac{cos(2^{\circ}-47^{\circ})+cos(2^{\circ}+47^{\circ})}{2}}=$

$=-\dfrac{2 \cdot sin45^{\circ}}{cos(-45^{\circ})+cos49^{\circ}}=-\dfrac{2 \cdot \dfrac{\sqrt{2}}{2}}{cos45^{\circ}+cos49^{\circ}}=-\dfrac{\sqrt{2}}{cos45^{\circ}+cos49^{\circ}};$

$1+tg2^{\circ} \cdot tg47^{\circ}=1+\dfrac{cos(2^{\circ}-47^{\circ})-cos(2^{\circ}+47^{\circ})}{cos(2^{\circ}-47^{\circ})+cos(2^{\circ}+47^{\circ})}=1+\dfrac{cos45^{\circ}-cos49^{\circ}}{cos45^{\circ}+cos49^{\circ}};$

$\dfrac{-\dfrac{\sqrt{2}}{cos45^{\circ}+cos49^{\circ}}}{1+\dfrac{cos45^{\circ}-cos49^{\circ}}{cos45^{\circ}+cos49^{\circ}}}=\dfrac{-\sqrt{2}}{cos45^{\circ}+cos49^{\circ}+cos45^{\circ}-cos49^{\circ}}=-\dfrac{\sqrt{2}}{2 \cdot cos45^{\circ}}=$

$=-\dfrac{\sqrt{2}}{2 \cdot \dfrac{\sqrt{2}}{2}}=-\dfrac{\sqrt{2}}{\sqrt{2}}=-1;$

__________________________________________________________

$tg \bigg (\dfrac{\pi}{6}+a \bigg )+tg \bigg (\dfrac{\pi}{6}-a \bigg )=\dfrac{sin \bigg (\dfrac{\pi}{6}+a+\dfrac{\pi}{6}-a \bigg )}{cos \bigg (\dfrac{\pi}{6}+a \bigg ) \cdot cos \bigg (\dfrac{\pi}{6}-a \bigg )}=$

$=\dfrac{sin \bigg (\dfrac{\pi}{3} \bigg )}{\dfrac{cos \bigg (\dfrac{\pi}{6}+a - \bigg (\dfrac{\pi}{6}-a \bigg ) \bigg )+cos \bigg (\dfrac{\pi}{6}+a+\dfrac{\pi}{6}-a \bigg )}{2}}=$

$=\dfrac{2 \cdot \dfrac{\sqrt{3}}{2}}{cos(2a)+cos \bigg (\dfrac{\pi}{3} \bigg )}=\dfrac{\sqrt{3}}{cos(2a)+\dfrac{1}{2}};$

$1-tg \bigg (\dfrac{\pi}{6}+a \bigg ) \cdot tg \bigg (\dfrac{\pi}{6}-a \bigg )=1-\dfrac{cos \bigg (\dfrac{\pi}{6}+a - \bigg (\dfrac{\pi}{6}-a \bigg ) \bigg )-cos \bigg (\dfrac{\pi}{6}+a +\dfrac{\pi}{6}-a \bigg )}{cos \bigg (\dfrac{\pi}{6}+a - \bigg (\dfrac{\pi}{6}-a \bigg ) \bigg )+cos \bigg (\dfrac{\pi}{6}+a +\dfrac{\pi}{6}-a \bigg )}=$

$=1-\dfrac{cos(2a)-cos \bigg (\dfrac{\pi}{3} \bigg )}{cos(2a)+cos \bigg (\dfrac{\pi}{3} \bigg )}=1-\dfrac{cos(2a)-\dfrac{1}{2}}{cos(2a)+\dfrac{1}{2}};$

$\dfrac{\dfrac{\sqrt{3}}{cos(2a)+\dfrac{1}{2}}}{1-\dfrac{cos(2a)-\dfrac{1}{2}}{cos(2a)+\dfrac{1}{2}}}=\dfrac{\sqrt{3}}{cos(2a)+\dfrac{1}{2}-cos(2a)+\dfrac{1}{2}}=\dfrac{\sqrt{3}}{1}=\sqrt{3};$

__________________________________________________________

$\dfrac{sin21^{\circ}cos28^{\circ}+cos21^{\circ}sin28^{\circ}}{cos18^{\circ}cos31^{\circ}-sin18^{\circ}sin31^{\circ}}=\dfrac{sin(21^{\circ}+28^{\circ})}{cos(18^{\circ}+31^{\circ})}=\dfrac{sin49^{\circ}}{cos49^{\circ}}=tg49^{\circ};$

xDanielAngelx: Спасибо огромное)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Определи склонение и падеж существительных.В осиновом лесу наступил вечер.Слышен шум воды в ручье.Леса почти не видно.Только ели растут выше,и поэтому они заметнее на фоне вечернего неба.

Русский язык, 1 год назад

сочинение на тему: Учиться на ошибках или избегать их?

Алгебра, 2 года назад

Помогите пожалуйста, 8 класс, даю 35 баллов Решить три задания: 1. Вычислить: / - дробная черта а)1/2√256+1,5√0,64 б)6,5-3√4/9 в)(2√2,5)² 2. Найдите значение выражения: а)√0,16×64 б)√7×√28...

Қазақ тiлi, 2 года назад

Ойлан Неліктен ғарыш зымы- ранын жасауға металдың барлық түрін пайдалана бермейді?

Литература, 8 лет назад

почему роман дон кихот является пародией рыцарского...

Математика, 8 лет назад

спортсмен прыгнул в длину на 7 м 20 см это в 4 раза больше чем его рост Найдите рост спортсмена...