Отрезки, соединяющие середины противолежащих сторон выпуклого четырехугольника, равны. Докажите, что диоганали этого четырехугольника перпендикулярны
Ответы на вопрос
Ответил Hrisula
0
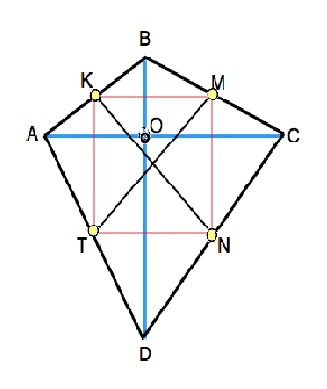
Пусть дан четырёхугольник АВСD. Точка К - середина АВ, т.М - середина ВС, N и Т - середины СD и DA соответсвенно. По условию КN=ТМ. Проведем диагонали АС и ВD. Соединим середины сторон треугольников АВС, ВСD, CDA и DAB. В треугольниках АВС и АDC средние линии параллельны и равны половине диагонали АС исходного четырехугольника.⇒ КМ параллельна и равна ТN. Аналогично доказывается КТ=МN. Противоположные стороны КМNТ параллельны и равны. КМNТ - параллелограмм с равными диагоналями ( КN=МТ по условию), т.е. КМNТ - прямоугольник. А раз стороны КМNТ пересекаются под прямым углом, то и диагонали четырехугольника АВСD, которым они параллельны, также пересекаются под прямым углом, ч.т.д.
Приложения:
Ответил Anya2350
0
Огромное вам спасибо за понятный ответ)
Ответил Hrisula
0
Хорошо, что всё понятно. Понятное решение запомнится.
Новые вопросы