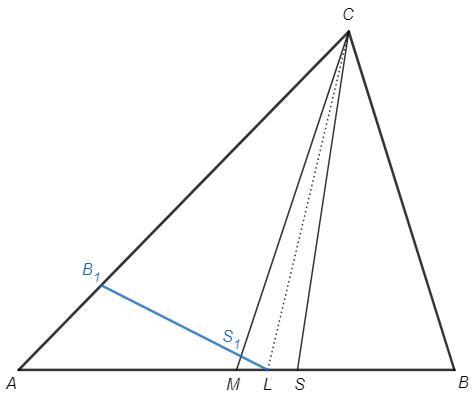
Отрезки CM, CL - соответственно медиана и биссектриса треугольника ABC, точка S на стороне AB
такова, что угол MCL =углу LCS (точка L лежит между М и Ѕ). Найдите BS, если AB = 14, BL = 6. Если
ответ является дробным числом, то его необходимо записать в виде десятичной дроби с запятой,
например, «0,15»​

AM=7, ML=1

По теореме о биссектрисе

AC/BC =AL/BL =8/6 =4/3

Проведем LB1, ∠CLB1=∠CLB

△B1CL=△BCL (по стороне и прилежащим углам), B1L=BL, B1C=BC

△S1CL=△SCL (по стороне и прилежащим углам), LS1=LS => S1B1=SB

По теореме Менелая

AM/ML *LS1/S1B1 *B1C/CA =1

7/1 *LS1/S1B1 *3/4 =1

LS/SB =LS1/S1B1 =4/21

SB= 21/25 BL =21*6/25 =5,04

Или метод площадей.

Площади треугольников с равными углами относятся как произведения сторон.

Площади треугольников с равными высотами относятся как основания.

S(ACM)/S(BCS) =4/3 *CM/CS

S(MCL)/S(SCL) =CM/CS

S(ACM)/S(BCS) =4/3 *S(MCL)/S(SCL)

S(MCL)/S(ACM) =1/7

LS/SB =S(SCL)/S(BCS) =4/3 *1/7