Алгебра, вопрос задал laninaa932 , 1 год назад

Отличники пожалуйста помогите c,d,e,f

Приложения:

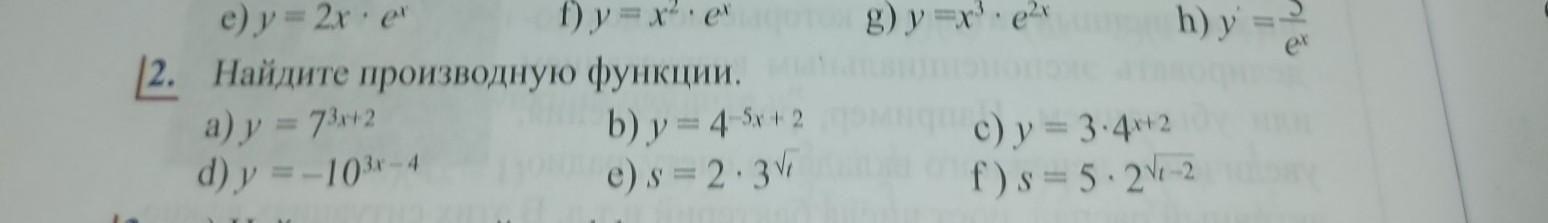
Ответы на вопрос

Ответил natalyabryukhova

1

Ответ:

a) $\displaystyle y'=3\;ln7\cdot\;7^{3x+2}$

b) $\displaystyle y'=-5\;ln4\cdot\;4^{-5x+2}$

c) $\displaystyle y'=3\;ln4\cdot\;4^{x+2}$

d) $\displaystyle y'=-3\;ln10\cdot\;10^{3x-4}$

e) $\displaystyle y'=\frac{3^{\sqrt{t}}\;ln3 }{\sqrt{t} }$

f) $\displaystyle y'=\frac{5^{\sqrt{t-2}}\;ln2 }{2\sqrt{t-2} }$

Объяснение:

Найти производную функции.

Формулы:

$\boxed {\displaystyle \bf (a^u)'=a^u\cdot ln\;a\cdot u'}$ $\boxed {\displaystyle \bf (x^n)'=nx^{n-1}}$

$\displaystyle \bf a) \;y=7^{3x+2}$

$\displaystyle y'=7^{3x+2}ln7\cdot (3x+2)'=7^{3x+2}ln\;7\cdot 3=3\;ln7\cdot\;7^{3x+2}$

$\displaystyle \bf b) \;y=4^{-5x+2}$

$\displaystyle y'=4^{-5x+2}ln4\cdot (-5x+2)'=4^{-5x+2}ln\;4\cdot (-5)=-5\;ln4\cdot\;4^{-5x+2}$

$\displaystyle \bf c) \;y=3\cdot 4^{x+2}$

$\displaystyle y'=3\cdot 4^{x+2}ln4\cdot (x+2)'=3\cdot 4^{x+2}ln\;4\cdot 1=3\;ln4\cdot\;4^{x+2}$

$\displaystyle \bf d) \;y=-10^{3x-2}$

$\displaystyle y'=(-1)\cdot 10^{3x-4}ln10\cdot (3x-4)'=(-1)\cdot 10^{3x-4}ln\;10\cdot 3=-3\;ln10\cdot\;10^{3x-4}$

$\displaystyle \bf e) \;s=2\cdot 3^{\sqrt{t} }=2\cdot 3^{t^{\frac{1}{2} }}$

$\displaystyle y'=2\cdot 3^{t^{\frac{1}{2} }}ln3\cdot (t^{\frac{1}{2} })'=2\cdot 3^{t^{\frac{1}{2} }}ln3\cdot \frac{1}{2}t^{-\frac{1}{2} } =\frac{3^{\sqrt{t}}\;ln3 }{\sqrt{t} }$

$\displaystyle \bf f) \;s=5\cdot 2^{\sqrt{t-2} }=5\cdot 2^{(t-2)^{\frac{1}{2} }$

$\displaystyle y'=5\cdot 2^{(t-2)^{\frac{1}{2} }}ln2\cdot ((t-2)^{\frac{1}{2} })'=5\cdot 2^{(t-2)^{\frac{1}{2} }}ln2\cdot \frac{1}{2}(t-2)^{-\frac{1}{2} } =\frac{5^{\sqrt{t-2}}\;ln2 }{2\sqrt{t-2} }$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Химия, 1 год назад

що є зайвим у переліку властивостей заліза: запах ,прозорість, тепловідність, електропровідність...

История, 1 год назад

помогитегиье пж я вообще не поняла что делать...

Українська література, 1 год назад

Літературний напрям твору "Думи мої, думи мої"...

Математика, 1 год назад

Помогите пожалуйста, кто поможет буду благодарна...

Русский язык, 6 лет назад

248Б. Составьте "словесный портрет" союза потому что.

Английский язык, 6 лет назад

Help pls! I will give 15 points...