острый угол параллелограмма равен 60 градусов. Меньшая диагональ наклонена к большей стороне под углом 30 Найдите площадь параллелограмма если больше его сторона равна 20

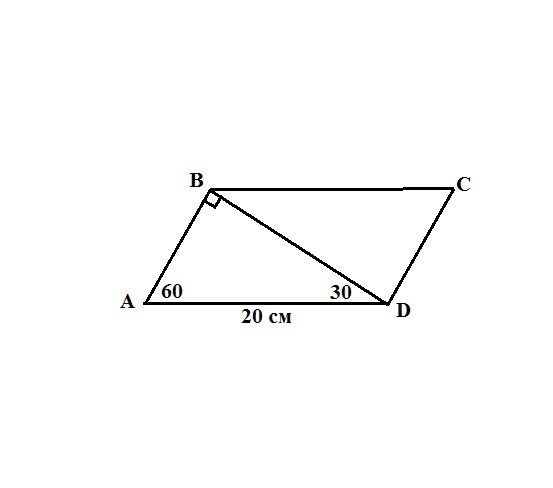
Дано: АВСD - параллелограмм
         АD = 20 см.
        ∠ ВАD = 60°
        ∠АDВ  = 30°
Найти: 
Решение:
∠ ВАD = 60°, ∠АDВ  = 30° (по условию) ⇒∠АВD = 180°-60°-30°=90°,т.е. прямой.
ΔАВD - прямоугольный.
Катет, лежащий против угла в 30° равен половине гипотенузы ⇒ АВ=AD:2=20:2=10 см.
S = AD*АВ=20*10=200 см²

спасиб

Пожалуйста