Острые углы прямоугольного треугольника равны 69 и 21 градус. Найти угол между ВЫСОТОЙ и МЕДИАНОЙ, проведёнными из вершины прямого угла.
Ответы на вопрос
Ответил Пеппер
8
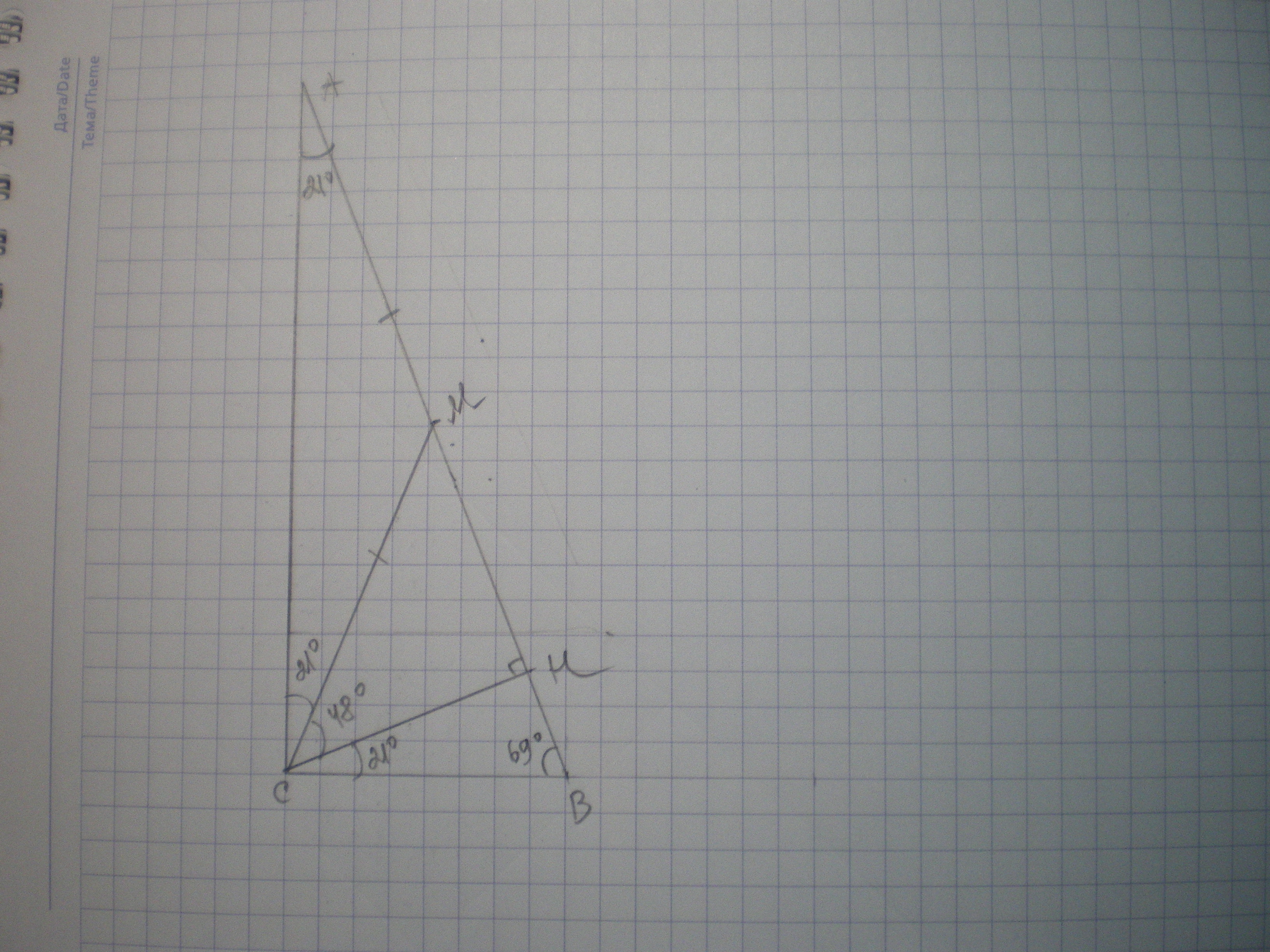
Дано: ΔАВС - прямоугольный, ∠С=90°, ∠В=69°, ∠А=21°, СН - высота, СМ - медиана. Найти ∠МСН.
Решение: в прямоугольном треугольнике медиана, проведенная из вершины прямого угла к гипотенузе, равна половине гипотенузы. Отсюда ΔАМС - равнобедренный, АМ=МС, тогда ∠АСМ=∠САМ=21°.
ΔСВН - прямоугольный, ∠ВСН=90-69=21°.
∠МСН=∠АСВ-∠АСМ-∠ВСН=90-21-21=48°.
Ответ: 48°.
Приложения:
Новые вопросы
Немецкий язык,
1 год назад
Українська мова,
1 год назад
Русский язык,
1 год назад
Биология,
7 лет назад