Основою прямого паралелепіпеда є ромб з діагоналями 6 і 8см. Діагональ бічної грані дорівнює √61см. Знайти більшу діагональ паралелепіпеда і площу повної поверхні.​

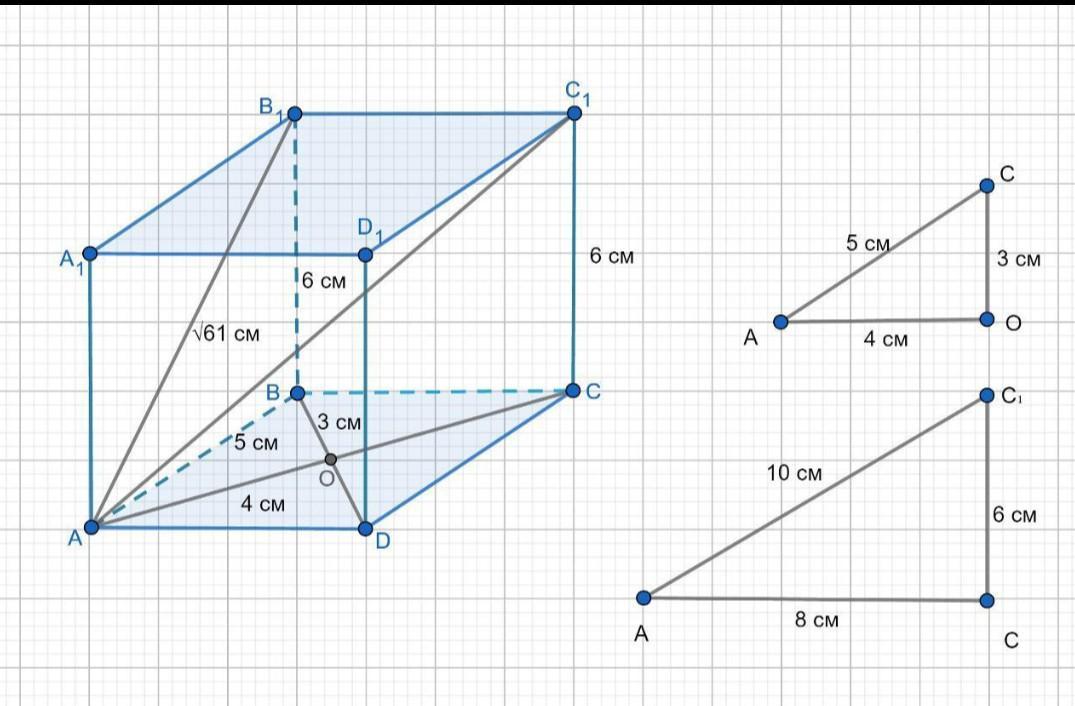
Діагоналі ромба припиняються під прямим кутом і точкою перетину діляться навпіл. В основі паралелепіпеда ромб, ДАОВ прямокутний, катет АО = 8/2 = 4 см, катет BO = 6/2 = 3 см. Знайдемо бік ромба АС по т. Піфагора з ДАОВ.

AB² = AO2 + OC² = 42 + 32 = 16+ 9 = 25; АВ = 5 СМ;

З ДАВВ, знайдемо висоту паралелепіпеда по т. Піфагора.

B,B2 = AB, AB² = 61-25 = 36; В₁B = 6 см;

З ДАРС, знайдемо велику діагональ паралелепіпеда АС, ² = АС ² + CC, ² = 82 + 6 ² = 64 +36 = 100;

Велика діагональ паралелепіпеда АС₁= 10 CM;

Бічна поверхня паралелепіпеда твору периметра основи

висоту паралелепіпеда:

S = P * H = 4 * 5 см * 6 см = 120 см ².