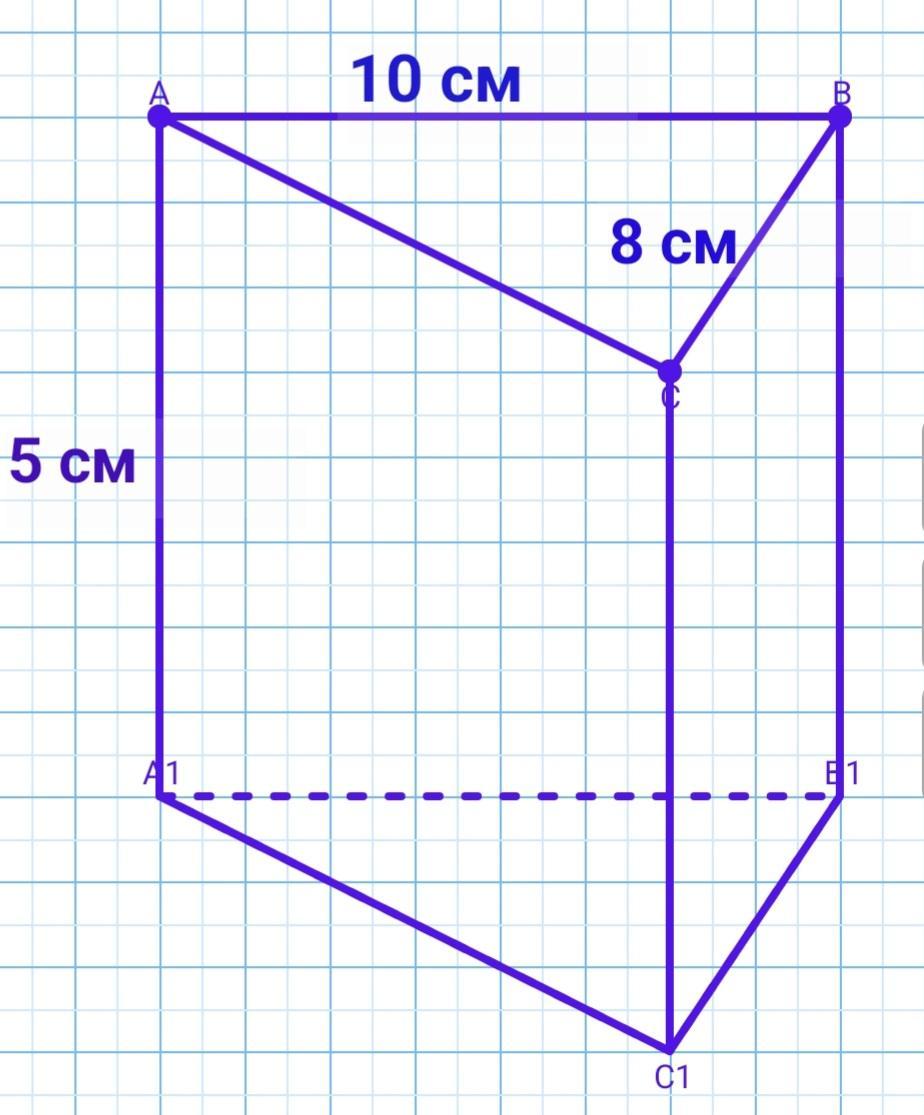
Основою прямої призми є прямокутний трикутник. один із катетів якого дорівнює 8 см, а гіпотенуза - 10 см. Бічне ребро призми дорівнює 5 см. Чому дорінює площа бічної поверхні призми?
Відповіді: А 240 см2 Б 70 см2 В 140 см2 Г 120 см2 Д 118 см2

Ответ:

Площа бічної поверхні прямої призми дорівнює 120 см² (Г)

Объяснение:

Основою прямої призми є прямокутний трикутник. один із катетів якого дорівнює 8 см, а гіпотенуза - 10 см. Бічне ребро призми дорівнює 5 см. Чому дорінює площа бічної поверхні призми?

Розв'язання:

Площу бічної поверхні прямої призми обчислюємо за формулою:

Sб=Poc•H,

де Poc – периметр основи;

H – висота прямої призми, довжина бічного ребра (АА1).

1)У прямокутному трикутнику ABC (∠C=90°), в якому BС=6 см – катет і АB=10 см – гіпотенуза, за теоремою Піфагора знайдемо катет BC:

AC²=АВ²-ВС²,

АС²= 10²-8²=100-64=36

АС= 6 см

2) Обчислимо периметр основи прямої призми:

Poc=AB+BC+AC=10+8+6= 24 см.

3) Обчислимо площу бічної поверхні прямої призми з бічним ребром H=АА1=5 см:

Sб=Poc•H =24•5=120 см²

Відповідь: 120 см²

#SPJ1