Основою прямої призми ABCDA1B1C1D1 є рівнобічна трапеція , основи якої BC і AD відповідно дорівнюють 11 см і 21 см, а бічна сторона – 13 см. Площа діагонального перерізу призми дорівнює 180 см^2. Знати площу бічної поверхні призми.

Ответ:

Площадь боковой поверхности призмы равна 522 см².

Объяснение:

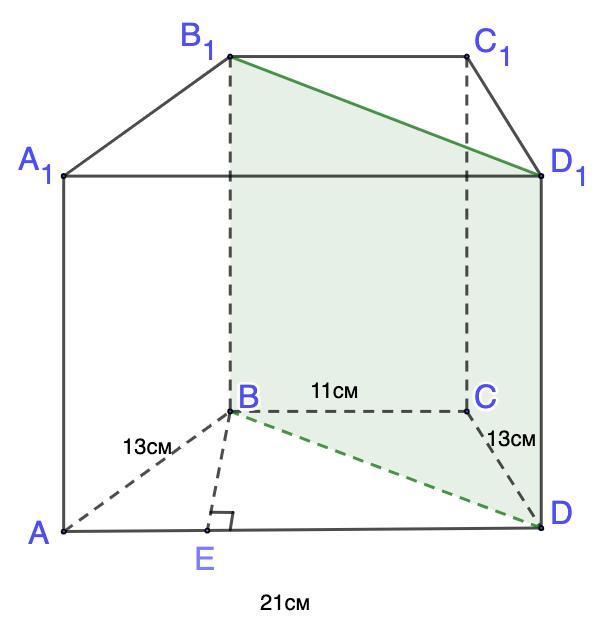
Основой прямой призмы ABCDA₁B₁C₁D₁ является равнобедренная трапеция, основания которой BC и AD соответственно равны 11 см и 21 см, а боковая сторона – 13 см. Площадь диагонального сечения призмы равна 180 см². Найти площадь боковой поверхности призмы.

Дано: ABCDA₁B₁C₁D₁ - прямая призма.

ABCD - равнобедренная трапеция;

BC = 11 см; AD = 21 см; АВ = CD = 13 см.

BB₁D₁D - диагональное сечение; S(BB₁D₁D) = 180 см²

Найти: Sбок

Решение:

Из вершины В опустим высоту ВЕ на основание AD.

Рассмотрим ABCD - равнобедренная трапеция.

• Высота, опущенная из вершины тупого угла равнобедренной трапеции на большее основание, делит его на части, меньшая из которых равна полуразности оснований.

⇒ АЕ = (AD - BC) : 2 = (21 - 11) : 2 = 5 (см)

Рассмотрим ΔАВЕ - прямоугольный.

• Теорема Пифагора:
• Квадрат гипотенузы равен сумме квадратов катетов.

⇒ АВ² = АЕ² + ВЕ²   ⇒   ВЕ² = 169 - 25 = 144   ⇒   ВЕ = 12 см

Рассмотрим ΔEBD - прямоугольный.

ED = AD - AE = 21 - 5 = 16 (см)

По теореме Пифагора:

BD² = ED² + BE² = 256 + 144 = 400   ⇒ BD = 20 см

Рассмотрим BB₁D₁D  - прямоугольник.

• Площадь треугольника равна произведению смежных сторон.

⇒  S(BB₁D₁D) = BD · DD₁

180 = 20 · DD₁   ⇒  DD₁ = 180 : 20 = 9 (см)

• Площадь боковой поверхности призмы равна:

      Sбок = Росн · Н,

где Н - высота призмы.

• Периметр - сумма длин всех сторон.

Росн = 13 + 11 + 13 + 21 = 58 (см); Н = DD₁ = 9 см

Sбок = 58 · 9 = 522 (см²)

Площадь боковой поверхности призмы равна 522 см².