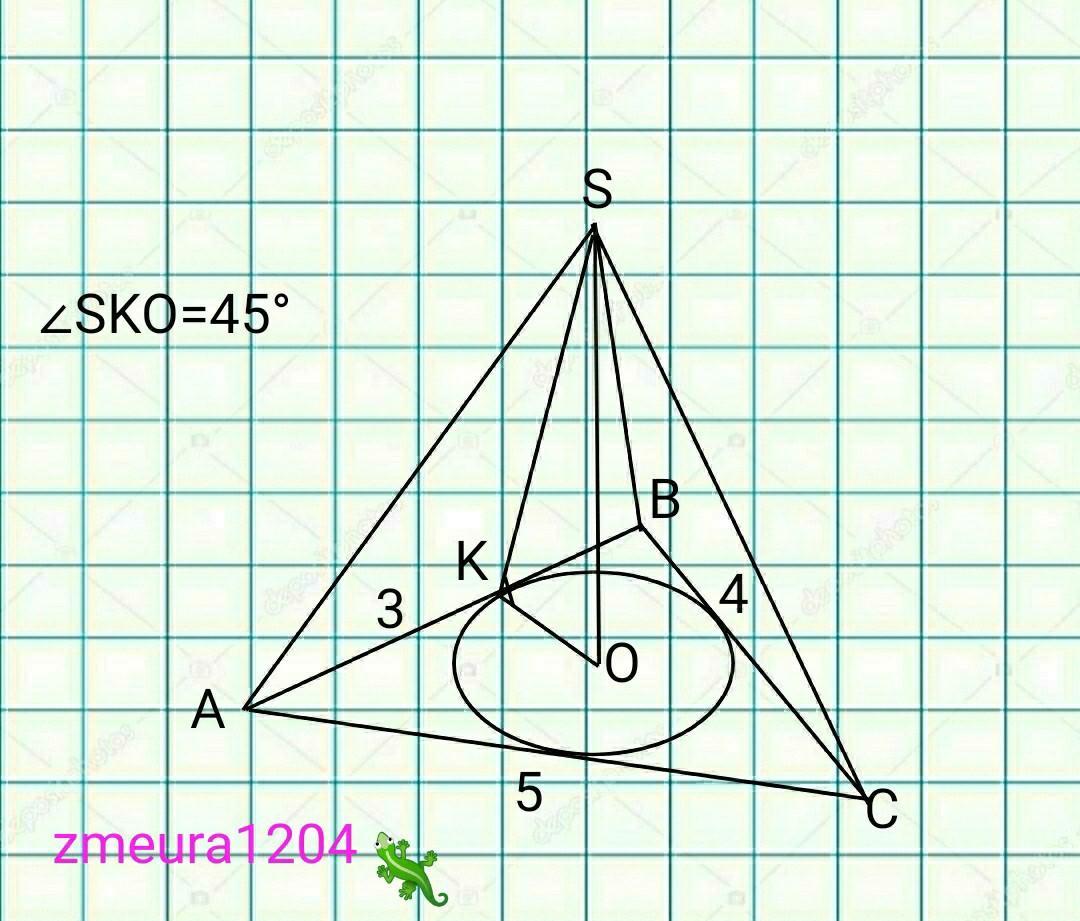
Основою піраміди є прямокутний трикутник з катетами 3 см і 4 см. Усі бічні грані піраміди утворюють із площиноЮ основи кути по 45°. Знайдіть площу бічної поверхні піраміди.
Ответы на вопрос
Ответил zmeura1204
8
Ответ:
Sбіч=6√2 см²
Объяснение:
∆ABC- прямокутний трикутник.
За теоремою Піфагора:
АС=√(АВ²+ВС²)=√(3²+4²)=5см
ОК=r.
r=(AB+BC-AC)/2=(3+4-5)/2=1см
∆SKO- прямокутний, рівнобедрений трикутник.
∠SOK=90°; ∠SKO=45°, за умови.
∠КSO=90°-∠SKO=90°-45°=45°, кути при основі рівні.
КО=SO=1 см.
За теоремою Піфагора:
SK=√(KO²+SO²)=√(1²+1²)=√2 см
Росн=АВ+ВС+АС=3+4+5=12см.
Sбіч=½*Росн*SK=½*12*√2=6√2 см²
Приложения:
zmeura1204:
Де ви бачите правильну піраміду?
АВ=3; ВС=4; АС=5
ну так, а ви використовуєте формулу для правильної піраміди
так все правильно. У основі правильної піраміди лежить правильний многокутник, а провильний многокутник той у який можна вписати коло, а у прямокутний трикутник можна вписати коло.
В любий трикутник можна вписати коло.
Я не розумію чим вам не подобається ця формула?
так все добре , я підтримую тебе . дякую за розв'язання
у будь-який трикутник можна вписати коло, але це не означає, що він правильний. прямокутний трикутник не правильний
Я і не казала, що він правильний.
усі грані нахиляються під одним кутом, тож проекція вершини такої піраміди є точка центру кола. І при цьому усі апофеми граней рівні.
Новые вопросы