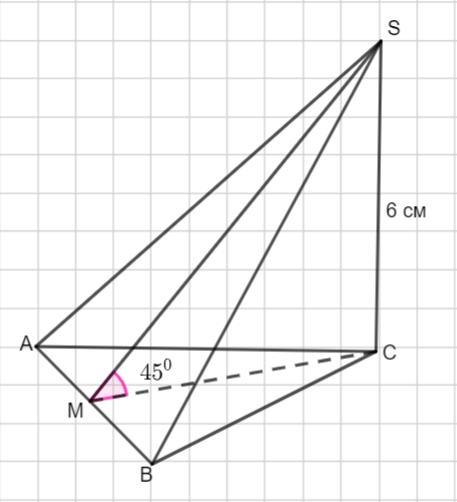
Геометрия, вопрос задал annadavidenko57 , 6 лет назад

Основою піраміди є правильний трикутник. Дві бічні грані пірвміди перпендикулярні до площини основи, а їх спільне бічне ребро дорівнює 6 см. Третя грань піраміди нахилена до площини основи під кутом 45 градусів. Знайдіть обєм піраміди?

Ответы на вопрос

Ответил lilyatomach

Ответ:

Объем пирамиды равен 24√3 см³

Объяснение:

Пусть дана пирамида $SABC$

Основание пирамиды Δ АВС- правильный. Грани Δ SBC и Δ SAC перпендикулярны плоскости основания, причем их общее боковое ребро SC=6 см. Это боковое ребро является высотой пирамиды. Третья грань наклонена к плоскости основания под углом 45°. Построим линейный угол двугранного угла. СМ ⊥ АВ ( СМ-высота треугольника Δ АВС ). По теореме о трех перпендикулярах SМ⊥ АВ и тогда ∠SМС угол наклона третьей грани. ∠SМС =45°.

Рассмотрим ΔSСМ - прямоугольный, если ∠SМС =45° и сумма острых углов прямоугольного треугольника равна 90°,

то ∠МSС =90°-45°=45°. ΔSСМ - прямоугольный, равнобедренный.

SС=МС =6 см.

Если СМ-высота треугольника правильного Δ АВС , то найдем сторону Δ АВС.

Высота равностороннего треугольника вычисляется по формуле

$h=\dfrac{a\sqrt{3} }{2} ,$ где a- сторона треугольника.

Тогда

$a=\dfrac{2h}{\sqrt{3} }$

$AB= \dfrac{2\cdot CM}{\sqrt{3} } ;\\\\AB= \dfrac{2\cdot 6}{\sqrt{3} }=\dfrac{12}{\sqrt{3} } =\dfrac{12\cdot \sqrt{3} }{\sqrt{3} \cdot\sqrt{3} }=\dfrac{12\sqrt{3} }{3}=4\sqrt{3}$