Основания равнобедренной трапеции равны 21 и 57, боковая
сторона равна 82. Найдите длину диагонали трапеции
Ответы на вопрос
Ответил KuOV
0
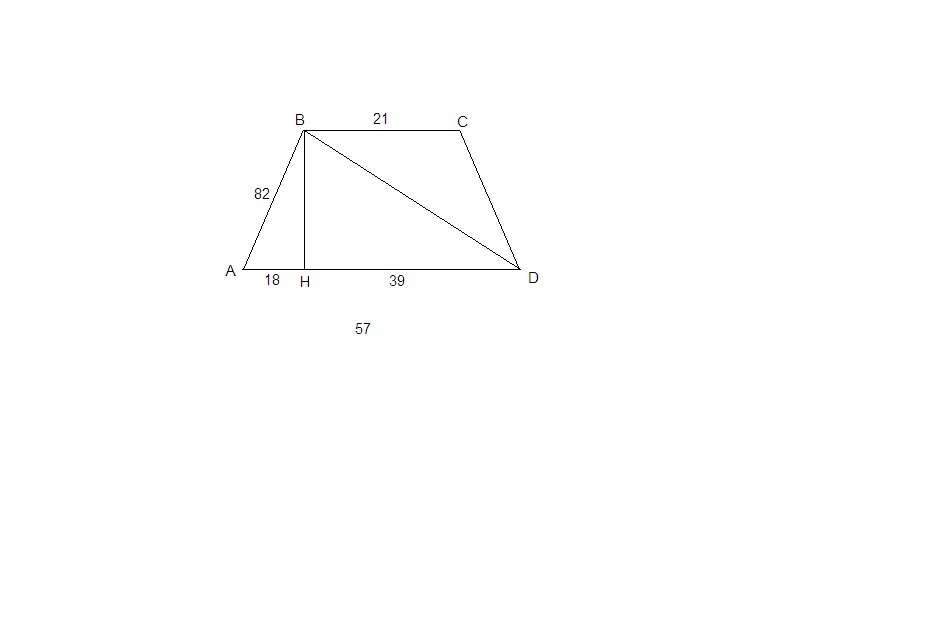
Проведем высоту ВН.
АН = (AD - BC)/2 = (57 - 21)/2 = 18 - так как трапеция равнобедренная.
HD = AD - АН = 57 - 18 = 39
ΔАВН: ∠АНВ = 90°, по теореме Пифагора
ВН = √(АВ² - АН²) = √((82 - 18)(82 + 18)) = √(64 · 100) = 8 · 10 = 80
ΔBHD: по теореме Пифагора
BD = √(BH² + HD²) = √(6400 + 1521) = √7921 = 89
АН = (AD - BC)/2 = (57 - 21)/2 = 18 - так как трапеция равнобедренная.
HD = AD - АН = 57 - 18 = 39
ΔАВН: ∠АНВ = 90°, по теореме Пифагора
ВН = √(АВ² - АН²) = √((82 - 18)(82 + 18)) = √(64 · 100) = 8 · 10 = 80
ΔBHD: по теореме Пифагора
BD = √(BH² + HD²) = √(6400 + 1521) = √7921 = 89
Приложения:
Новые вопросы